Задача 1:
В треугольнике ABC провели все медианы. Оказалось, что у четырех
из шести полученных треугольников равны радиусы описанных окружностей.
Верно ли, что треугольник ABC
а) равнобедренный?
б) равносторонний?
Задача 2:
Обозначим
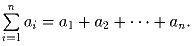
Известно, что
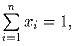
и
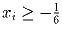
при любом i = 1,2, … ,n. Докажите неравенство:
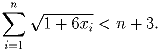
Задача 3:
В турнире, проходящем по олимпийской системе (с выбыванием),
участвуют 512 теннисистов. Перед началом турнира каждому участнику
присвоен номер от 1 до 512 в соответствии с его рейтингом. Матч
считается неинтересным, если разность присвоенных номеров двух
спортсменов, участвующих в нем, больше 30. Докажите, что независимо
от жеребьевки и результатов игр, будет сыгран хотя бы один
неинтересный матч.
Задача 4:
100 первых натуральных чисел в каком-то порядке записали в ряд и
вычислили 98 сумм, получаемых при сложении троек подряд идущих чисел.
Какое наибольшее количество нечетных сумм может получиться?


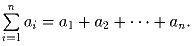 Известно, что
Известно, что 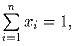 и
и 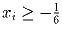 при любом i = 1,2, … ,n. Докажите неравенство:
при любом i = 1,2, … ,n. Докажите неравенство: