 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 10 класс >> 2-й день | Убрать решения |
|
|
| XXXVI Екатеринбургская городская олимпиада, 1995-1996. Областной тур. 10 класс. 2-й день |
|
|
а) равнобедренный?
б) равносторонний?
Решение: Без ограничения общности, пусть у треугольников BOA1 и COA1 (cм. рис.13) равны радиусы описанных окружностей. Так как их площади равны (OA1 – медиана треугольника BOC), из формулы
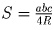 (a, b, c, – cтороны треугольника,
S и R – площадь и радиус описанной окружности соответственно)
получаем равенство отрезков BO и CO, что обеспечивает
равнобедренность ABC. Далее возможны два случая: 1) равные радиусы
описанных окружностей имеют треугольники BOA1 и BOC1 и
2) треугольники BOA1 и AOB1. В первом случае, так как
треугольник BOA1 прямоугольный, отрезок OB является
диаметром окружности описанной около четырехугольника OA1BC1,
поэтому CC1 – высота ABC, и треугольник правильный.
Во втором случае из уже упоминавшейся формулы
(a, b, c, – cтороны треугольника,
S и R – площадь и радиус описанной окружности соответственно)
получаем равенство отрезков BO и CO, что обеспечивает
равнобедренность ABC. Далее возможны два случая: 1) равные радиусы
описанных окружностей имеют треугольники BOA1 и BOC1 и
2) треугольники BOA1 и AOB1. В первом случае, так как
треугольник BOA1 прямоугольный, отрезок OB является
диаметром окружности описанной около четырехугольника OA1BC1,
поэтому CC1 – высота ABC, и треугольник правильный.
Во втором случае из уже упоминавшейся формулы 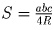 получаем
равенство отрезков BA1 и AB1 (здесь использовался факт, что
медианы в точке пересечения делятся в отношении 2:1), что опять
показывает правильность треугольника ABC.
получаем
равенство отрезков BA1 и AB1 (здесь использовался факт, что
медианы в точке пересечения делятся в отношении 2:1), что опять
показывает правильность треугольника ABC.Задача 2: Обозначим
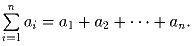 Известно, что
Известно, что 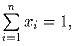 и
и 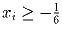 при любом i = 1,2, … ,n. Докажите неравенство:
при любом i = 1,2, … ,n. Докажите неравенство: 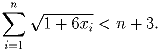
Решение: Так как при всех
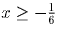 выполнено
выполнено
 имеем:
имеем:
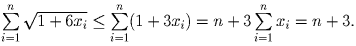 Остается заметить, что равенство
невозможно, так как хотя бы одно xi обязано быть положительным.
Задача 3:
В турнире, проходящем по олимпийской системе (с выбыванием),
участвуют 512 теннисистов. Перед началом турнира каждому участнику
присвоен номер от 1 до 512 в соответствии с его рейтингом. Матч
считается неинтересным, если разность присвоенных номеров двух
спортсменов, участвующих в нем, больше 30. Докажите, что независимо
от жеребьевки и результатов игр, будет сыгран хотя бы один
неинтересный матч.
Остается заметить, что равенство
невозможно, так как хотя бы одно xi обязано быть положительным.
Задача 3:
В турнире, проходящем по олимпийской системе (с выбыванием),
участвуют 512 теннисистов. Перед началом турнира каждому участнику
присвоен номер от 1 до 512 в соответствии с его рейтингом. Матч
считается неинтересным, если разность присвоенных номеров двух
спортсменов, участвующих в нем, больше 30. Докажите, что независимо
от жеребьевки и результатов игр, будет сыгран хотя бы один
неинтересный матч.Решение: Предположим, что удалось провести турнир без неинтересных матчей. Тогда в первом туре участник с номером 1 играл с теннисистом, номер которого не более 31, поэтому наименьший номер среди теннисистов, прошедших во второй тур не более 31. Аналогично, наибольший номер среди этих участников не менее 482. К третьему туру эти номера будут 61 и 452, к четвертому – 91 и 422 и.т.д. К последнему девятому туру останется два игрока: один с номером не более 241, второй с номером не менее 272. В этом случае финальный матч неинтересен, что противоречит предположению. Задача 4: 100 первых натуральных чисел в каком-то порядке записали в ряд и вычислили 98 сумм, получаемых при сложении троек подряд идущих чисел. Какое наибольшее количество нечетных сумм может получиться?
Решение: Если сначала записать 75 чисел в порядке ччнччнччн … ччн (здесь «ч» обозначает четное число, «н» – нечетное), а затем оставшиеся 25 нечетных чисел, то все суммы кроме одной окажутся нечетными. Покажем, что хотя бы одна четная сумма встретится. Пусть это не так. Тогда в зависимости от четности чисел, стоящих на первом и втором месте, возникает одна из четырех последовательностей: 1) нннн … нн, 2) нччнчч … нччн, 3) чнччнч … чнчч и 4) ччнччн … ччнч, однако ни в одной из них не получается поровну четных и нечетных чисел, поэтому все они нелегальны.
Ответ: 97 сумм.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 10 класс >> 2-й день | Убрать решения |