 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |
|
|
| XXXVI Екатеринбургская городская олимпиада, 1995-1996. Областной тур. 11 класс. 2-й день |
|
|
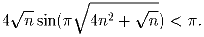
Решение: Используя периодичность функции sin x и то, что при всех x ≥ 0 sin x ≤ x, имеем цепочку неравенств, которая доказывает утверждение задачи:
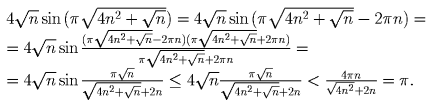
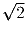 можно
расставить на доске 7 × 7 клеток так, чтобы внутри каждой
клетки хотя бы одна точка была покрыта некоторой фишкой?
(Длина стороны клетки равна 1).
можно
расставить на доске 7 × 7 клеток так, чтобы внутри каждой
клетки хотя бы одна точка была покрыта некоторой фишкой?
(Длина стороны клетки равна 1).Решение:
Заметим, (см. рис.14.) что одна фишка не может покрыть одновременно точки, лежащие внутри любых закрашенных клеток доски , так как расстояние между такими точками больше, чем диаметр фишки. Значит, для того, чтобы задействовать все закрашенные клетки, потребуется не менее 9 фишек. 9 фишек достаточно. В самом деле, одну фишку можно разместить таким образом, что в каждой клетке некоторого прямоугольника 2 × 3 найдется точка, покрытая этой фишкой. Покрыть доску 7 × 7 девятью такими прямоугольниками труда не составляет.
Ответ: 9 фишек.
Задача 3: Решите в целых числах уравнение: y³ = x6 + 2x4 – 1000.Решение:
Очевидно, пара x = 0, y = – 10 – решение. Покажем, что других решений нет. Случаи x = ± 1, x = ± 2, x = ± 3, и x = ± 4 проверяются непосредственно. Если же | x | ≥ 5, то 2x4 > 1000, поэтому x6 + 2x4 – 1000 > (x²)³. С другой стороны, для всех x x6 + 2x4 – 1000 < (x² + 1)³. Значит, при всех x по модулю больших 4 выполнено неравенство: x² < y < x² + 1, невозможное для натуральных x и y.
Задача 4: В единичном кубе (рис.3) пропилены 3 сквозных отверстия в форме прямоугольных параллелепипедов, основаниями которых являются квадраты (рис.4) с диагоналями, расположенными на средних линиях граней. Диагонали квадратов равны ½. Определите объем «дырявого» куба.Решение: Найдем объем ⅛ части куба (см. рисунок). Он равен
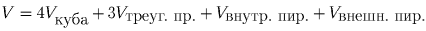 (рис.16–19).
Имеем:
(рис.16–19).
Имеем: 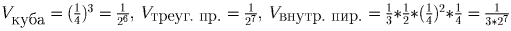 . В правильной треугольной пирамиде (мы ее условно
назовем внешней) основание равно
. В правильной треугольной пирамиде (мы ее условно
назовем внешней) основание равно 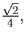 боковое ребро
равно половине диагонали куба с ребром равным ¼. Радиус
описанной окружности основания пирамиды равен
боковое ребро
равно половине диагонали куба с ребром равным ¼. Радиус
описанной окружности основания пирамиды равен 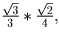 поэтому высота пирамиды h вычисляется по теореме
Пифагора:
поэтому высота пирамиды h вычисляется по теореме
Пифагора:  .
Отсюда
.
Отсюда 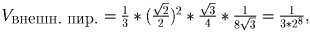

 .
.Ответ: 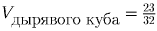 .
.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |