Задача 1:
В выпуклом многоугольнике каждый внутренний угол измеряется
целым числом градусов. Докажите, что число сторон этого многоугольника
не превосходит 360.
Решение: Пусть n – число сторон такого многоугольника. Тогда
сумма его внутренних углов равна S = 180°(n – 2).
В силу условия каждый внутренний угол многоугольника не
превосходит 179°, поэтому S ≤ 179°n. Из неравенства
180°(n – 2) ≤ 179°n следует, что n
не превосходит 360.
Задача 2:
Пусть a ≥ 0, b ≥ 0, c ≥ 0, d ≥ 0, c + d ≤ a, c + d ≤ b. Докажите, что ad + bc ≤ ab.
Решение:
Перемножая почленно неравенства c ≤ a – d и d ≤ b – c (это
делать можно, так как обе части нервенств неотрицательны), немедленно
получаем требуемое утверждение.
Задача 3:
Двое движутся по окружности навстречу друг другу. Один пробегает
окружность за 3 минуты, а другой – за 5 минут. Через сколько минут
происходит каждая встреча?
Решение:
Пусть l – длина окружности, и t – время между встречами.
Тогда скорости бегунов равны
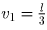
и

cоответственно, поэтому

откуда
t = 1⅞ мин.
Задача 4:
Решите в целых числах уравнение:
4x³ = 2y³ + z³.
Решение:
Пусть x
0, y
0, z
0 – некоторое решение данного
уравнения. Тогда z
0 четно, т.е. z
0 = 2z
1 для некоторого
целого z
1. Отсюда
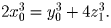
Рассуждая аналогично, получим: y
0 = 2y
1 и x
0 = 2x
1, причем
числа x
1, y
1, z
1 удовлетворяют исходному уравнению.
Продолжая этот процесс, получаем, что числа x
0, y
0, z
0
делятся на 4, на 8, на 16 и вообще на любую степень числа 2. Это
возможно только при x
0 = y
0 = z
0 = 0.
Ответ: x = y = z = 0.


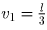 и
и  cоответственно, поэтому
cоответственно, поэтому  откуда
t = 1⅞ мин.
Задача 4:
Решите в целых числах уравнение:
4x³ = 2y³ + z³.
откуда
t = 1⅞ мин.
Задача 4:
Решите в целых числах уравнение:
4x³ = 2y³ + z³.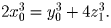 Рассуждая аналогично, получим: y0 = 2y1 и x0 = 2x1, причем
числа x1, y1, z1 удовлетворяют исходному уравнению.
Продолжая этот процесс, получаем, что числа x0, y0, z0
делятся на 4, на 8, на 16 и вообще на любую степень числа 2. Это
возможно только при x0 = y0 = z0 = 0.
Рассуждая аналогично, получим: y0 = 2y1 и x0 = 2x1, причем
числа x1, y1, z1 удовлетворяют исходному уравнению.
Продолжая этот процесс, получаем, что числа x0, y0, z0
делятся на 4, на 8, на 16 и вообще на любую степень числа 2. Это
возможно только при x0 = y0 = z0 = 0.