 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |
|
|
| XXXVI Екатеринбургская городская олимпиада, 1995-1996. Областной тур. 9 класс. 1-й день |
|
|
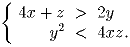
Решение: Приведем 2 решения.
1 решение: Рассмотрим квадратный трехчлен f(a) = xa² + ya + z. Его дискриминант y² – 4xz < 0, поэтому f(a) не имеет вещественных корней. В силу первого неравенства системы f( – 2) = 4x – 2y + z > 0, значит f(a) > 0 для всех действительных a. Остается заметить, что f(0) = z.
2 решение: От противного, пусть z ≤ 0. Случай z = 0 невозможен ввиду второго неравенства системы. Если z < 0, то из первого неравенства имеем 4xz < (2y – z)z. Тогда y² < 4x < 2zy – z², то есть (z – y)² < 0, что невозможно. Противоречие.
Задача 2: Требуется разрезать квадратный торт на n (n ≥ 6) квадратных кусков (не обязательно одинаковых). Для каких n это возможно?
Решение:
Ответ: для любого n. Способ разрезания указан на рис.5 для четного n и на рис.6 для нечетного n.
Задача 3: На горизонтальной поверхности лежат в ряд, касаясь друг друга, 100 одинаковых бревен, сплошь вымазанных дегтем. В ложбину между двумя самыми левыми бревнами кладут такое же, но чистое бревно и без проскальзывания катят его вправо до самой правой ложбины. Какая часть боковой поверхности этого бревна останется чистой к концу пути?Решение:
Рассмотрим поперечные срезы бревен (см. рисунок). Пусть O – центр катящегося бревна в начальном положении, P – его центр в тот момент, когда оно ляжет в следующую ложбину, O1, O2, O3 – центры первых трех неподвижных бревен. При перекатывании бревна в следующую ложбину на нем испачкается дуга BA1 = BA. Так как все треугольники O1OO2, OO2P, O2PO3, … правильные, дуга BA составляет 60°. Следующая испачканная дуга начнется с точки C и.т.д. Таким образом, испачканные дуги меры 60° чередуются с чистыми дугами той же меры.
Ответ: половина поверхности.
Задача 4: Пусть p – простое число, большее 3. Известно, что для некоторого натурального n запись числа pn содержит ровно 20 цифр. Докажите, что среди них найдутся 3 одинаковые цифры.Решение: Предположим противное, т.е. предположим, что среди цифр числа pn нет трех одинаковых. Тогда каждая цифра входит в это число ровно 2 раза, поэтому сумма цифр числа pn равна 2(0 + 1 + 2 + … + 9) = 90, откуда pn делится на 3. Но тогда и p делится на 3, чего быть не может, так как p – простое число, большее 3.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |