 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Районный тур >> 9 класс | Убрать решения |
|
|
| XXXVI Екатеринбургская городская олимпиада, 1995-1996. Районный тур. 9 класс |
|
|
Решение:
Непосредственно убеждаемся, что p = 3 удовлетворяет условию задачи. Пусть p ≠ 3. Тогда, так как p простое, p = 3n ± 1, и | p² – 22| = |9n² ± 6n – 21| делится на 3. Так как |p² – 22| – простое число, то оно равно 3, откуда p = 5.
Ответ: p = 3 или p = 5.
Задача 2: Докажите, что для всех положительных чисел a, b c и d выполнено неравенство: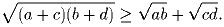
Решение:
Так как обе части неравенства неотрицательны, то после возведения
в квадрат полуаем равносильное
неравенство: 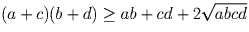 , которое сводится
к неравенству:
, которое сводится
к неравенству: 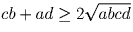 , которое справедливо, так
как среднее арифметическое не меньше среднего геометрического.
, которое справедливо, так
как среднее арифметическое не меньше среднего геометрического.
Решение: Пусть n0 – наименьшее из записанных чисел (такое число существует, так как все числа натуральные). Пусть ai, i ≤ 8 – его соседи. Имеем: ai ≥ n0, где i ≤ 8 и
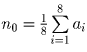 .
Отсюда все ai = n0. Рассужджая аналогично, получим, что числу n0
равны также и все соседи его соседей, и их соседи, и.т.д., значит
вообще все числа.
Задача 4:
На плоскости заданы отрезки длинами a см., b см., и 1 см.
С помощью циркуля и линейки отложить отрезки длиной
.
Отсюда все ai = n0. Рассужджая аналогично, получим, что числу n0
равны также и все соседи его соседей, и их соседи, и.т.д., значит
вообще все числа.
Задача 4:
На плоскости заданы отрезки длинами a см., b см., и 1 см.
С помощью циркуля и линейки отложить отрезки длинойа) 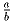 см.
см.
б) ab см.
Решение: Достаточно построить чертеж, как на рисунке. Пусть b < 1 (другие случаи аналогичны). Тогда если AC1 = b, AC = 1, C1B1 = a, то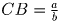 . Если же AC1 = a, CB = b, C1B1 = 1, то
AC = ab.
. Если же AC1 = a, CB = b, C1B1 = 1, то
AC = ab.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVI олимпиада, 1995-1996 >> Районный тур >> 9 класс | Убрать решения |