Задача 1: Найдите функцию f, определенную на всей числовой прямой и при всех x ≠ ½ удовлетворяющую уравнению:

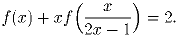
Решение: Пусть f – искомая функция, т.е. 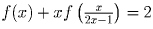при всех x ≠ ½. Положив в качестве x выражение 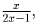получим: 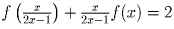. Имеем систему:

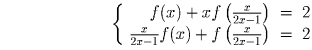
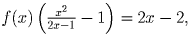. Умножим второе уравнение на x и вычтем из него первое. Имеем или 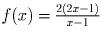. Эта функция определена при всех x ≠ 1. Подставив x = 1 в первое уравнение системы, найдем f(1) = 1.

ОТВЕТ: .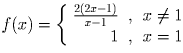

Задача 2: Точка K делит сторону BC треугольника ABC в отношении p:q, считая от вершины B. Точка F делит сторону AC в отношении  α : β , считая от вершины A. В каком отношении прямая BF делит отрезок AK?

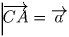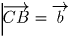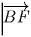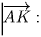
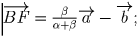
Решение: Пусть O – точка пересечения отрезков AK и BF (см. рисунок). Введем векторы и . Выразим через них векторы и 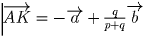. Пусть AO =  λ AK, OB =  μ BF. Тогда имеем:

откуда имеем систему:

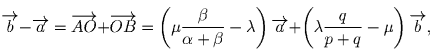
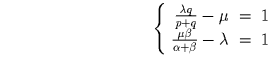
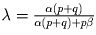. Решая ее, находим . Получаем ответ: .

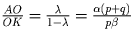Задача 3: Натуральные числа n, m и k (n < m < k) являются длинами сторон треугольника, один из углов которого равен 120°. Какое наименьшее значение может принимать n ?

Решение: Так как против угла в 120° лежит наибольшая сторона, имеем по теореме косинусов: k² = m² + n² – 2mn cos 120° = m² + n² + mn. При n = 1 имеем k² = m² + m + 1, откуда (m + 1)² > k² > m², что невозможно для целых чисел m и k. При n = 2: k² = m² + 2m + 4, откуда (m + 2)² > k² > (m + 1)², что также невозможно. Наконец, при n = 3 уравнение имеет решение (единственное!) в целых числах: m = 5, k = 7.

ОТВЕТ: n = 3.

Задача 4: На чемпионате мира по футболу 1994 года по окончании групповых игр (в группе 4 команды) очки, набранные командами одной из групп, образовали арифметическую прогрессию с разностью, отличной от нуля. Сколько очков набрала команда, занявшая третье место в этой группе?

Примечание: игры в группах проводились в один круг, победитель каждого матча получал 3 очка, проигравший – 0, а в случае ничьей каждая команда получала по 1 очку.

Решение: Пусть d – разность получившейся арифметической прогрессии (d > 0), a_i – число очков, набранное командой, занявшей i-ое место (i = 1,2,3,4). Тогда в сумме команды набрали 4a₄ + 6d очков. Всего было проведено 6 матчей, поэтому 4a₄ + 6d = 6*3 – n, где n – число ничьих. Из уравнения видно, что n четно. Кроме того, оно отлично от 6, так как не все встречи завершились вничью. При n = 4 получаем a₄ = 2, d = 1. При n = 2 – a₄ = 1, d = 2. Наконец, при n = 0 – либо a₄ = 0, d = 3, либо a₄ = 3, d = 1,. Последний вариант невозможен, так как при отсутствии ничьих все a_i делятся на 3. В остальных случаях a₃ = 3, поэтому третья команда набрала ровно 3 очка.

Примечание. На чемпионате мира 1994 года такая ситуация сложилась в группе B: 1. Бразилия – 7 очков, 2. Швеция – 5 очков, 3. Россия – 3 очка, 4. Камерун – 1 очко.