 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 10 класс >> 1-й день | Показать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 10 класс. 1-й день |
|
|
Найти все тройки ненулевых чисел
a, b и c, образующих арифметическую
прогрессию и таких, что из чисел 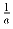 ,
, 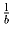 ,
, 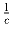 также можно составить арифметическую прогрессию.
также можно составить арифметическую прогрессию.
(Рекомендована жюри Российской олимпиады.)
Задача 2:Найдите тройки чисел a, b и c, являющиеся степенями пятёрки с целыми неотрицательными показателями, такие, что приписывая десятичную запись одного из них к десятичной записи другого, получим третье число.
(Рекомендована жюри Российской олимпиады.)
Задача 3:В вершинах и точках пересечения диагоналей правильного пятиугольника записаны нули. За один ход разрешается добавить + 1 или – 1 одновременно ко всем числам, расположенным на какой-либо из диагоналей пятиугольника. Какие из указанных на рисунках пятиугольников можно получить через несколько ходов?
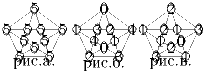
((Предложена С.Э.Нохриным.))
Задача 4:В остроугольном треугольнике ABC проведены высоты: AH, BK и CL. Найдите периметр треугольника HKL, если известны высота AH = h и угол ∠ BAC = α .
((Предложена В.Н.Ушаковым.))
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 10 класс >> 1-й день | Показать решения |