 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 10 класс >> 1-й день | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 10 класс. 1-й день |
|
|
Найти все тройки ненулевых чисел
a, b и c, образующих арифметическую
прогрессию и таких, что из чисел 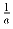 ,
, 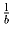 ,
, 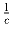 также можно составить арифметическую прогрессию.
также можно составить арифметическую прогрессию.
(Рекомендована жюри Российской олимпиады.)
Решение: По свойству арифметической прогрессии имеем a + c = 2b и одно из следующих уравнений
Ответ: – 2t, – 0,5t и t при t ≠ 0.
Задача 2:Найдите тройки чисел a, b и c, являющиеся степенями пятёрки с целыми неотрицательными показателями, такие, что приписывая десятичную запись одного из них к десятичной записи другого, получим третье число.
(Рекомендована жюри Российской олимпиады.)
Решение: Пусть a = 5n,b = 5m,c = 5k и в числе b, ровно t десятичных знаков. Имеем уравнение: 5n • 10t + 5m = 5k. Очевидно, m < k. Сократив уравнение на 5 в наибольшей степени, получим либо 2t + 5m – n – t = 5k – t, либо 5n – m + t • 2t + 1 = 5k – m. Первое уравнение имеет единственное решение в целых числах t = 2, m – n – t = 0, k – t = 1, откуда b = 25, m = 2, n = 0, k = 3 и искомые числа – 1, 25, 125. Второе уравнение выполняется только при n – m + t = 0, что приводит к предыдущему случаю.Ответ: 1, 25 и 125.
Задача 3:В вершинах и точках пересечения диагоналей правильного пятиугольника записаны нули. За один ход разрешается добавить + 1 или – 1 одновременно ко всем числам, расположенным на какой-либо из диагоналей пятиугольника. Какие из указанных на рисунках пятиугольников можно получить через несколько ходов?
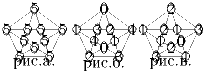
((Предложена С.Э.Нохриным.))
Решение: Занумеруем диагонали пятиугольника числами от 1 до 5, и пусть xi – число добавленных единиц к i-ой диагонали. Число в любой вершине (точке пересечения диагоналей) равно сумме чисел xi по всем i таким, что i-ая диагональ проходит через эту вершину (точку пересечения диагоналей). Имеем систему десяти уравнений с пятью неизвестными, которая оказывается несовместной во всех изображённых на рисунках случаях.Ответ: никакой пятиугольник получить нельзя.
Задача 4:В остроугольном треугольнике ABC проведены высоты: AH, BK и CL. Найдите периметр треугольника HKL, если известны высота AH = h и угол ∠ BAC = α .
((Предложена В.Н.Ушаковым.))
Решение: Прямые KL, KH и HL (см. рис.) отсекают от ∆ ABC треугольники, подобные ∆ ABC. Действительно, ∆ CHA ∽ ∆ CKB по I признаку подобия треугольников (2 равных угла). Отсюда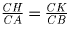 . Но тогда
∆ KHC ∽ ∆ BAC по II признаку подобия
треугольников (пропорциональность сторон и равенство углов между
этими сторонами). Аналогично доказывается, что ∆ AKL ∽ ∆ ABC и ∆ BHL ∽ ∆ ABC. Итак, имеем
∠ HLB = ∠ ALK = ∠ C, ∠ AKL = ∠ CKH = ∠ B.
Тогда точки H′ и H″, симметричные точке H относительно прямых
AB и AC, соответственно, лежат на прямой KL. Действительно,
∠ HLB = ∠ H′LB (т.к. ∆ HLO′ = ∆ H′LO′), но
∠ HLB = ∠ ALK, отсюда ∠ ALK = ∠ H′LB, а значит
точки K, L, H′ лежат на одной прямой. Аналогично доказывается,
что H″, K, L лежат на одной прямой. Отрезок H″H′ равен
периметру ∆ KLH (KH = KH″, и LH = LH′). Рассмотрим теперь
∆ H″AH′. Он равнобедренный, т.к. AH′ = AH = AH", а ∠ H″AH′ = 2 • ( ∠ CAH + ∠ BAH) = \ = 2 α . Отсюда H″H′ = 2AH′ sin \, α . Итак, периметр ∆ KLH равен 2h sin \, α .
. Но тогда
∆ KHC ∽ ∆ BAC по II признаку подобия
треугольников (пропорциональность сторон и равенство углов между
этими сторонами). Аналогично доказывается, что ∆ AKL ∽ ∆ ABC и ∆ BHL ∽ ∆ ABC. Итак, имеем
∠ HLB = ∠ ALK = ∠ C, ∠ AKL = ∠ CKH = ∠ B.
Тогда точки H′ и H″, симметричные точке H относительно прямых
AB и AC, соответственно, лежат на прямой KL. Действительно,
∠ HLB = ∠ H′LB (т.к. ∆ HLO′ = ∆ H′LO′), но
∠ HLB = ∠ ALK, отсюда ∠ ALK = ∠ H′LB, а значит
точки K, L, H′ лежат на одной прямой. Аналогично доказывается,
что H″, K, L лежат на одной прямой. Отрезок H″H′ равен
периметру ∆ KLH (KH = KH″, и LH = LH′). Рассмотрим теперь
∆ H″AH′. Он равнобедренный, т.к. AH′ = AH = AH", а ∠ H″AH′ = 2 • ( ∠ CAH + ∠ BAH) = \ = 2 α . Отсюда H″H′ = 2AH′ sin \, α . Итак, периметр ∆ KLH равен 2h sin \, α .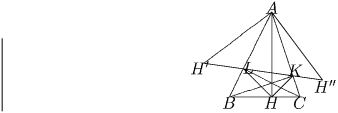
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 10 класс >> 1-й день | Убрать решения |