 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 10 класс >> 2-й день | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 10 класс. 2-й день |
|
|
Определённая на всей числовой прямой функция f(x) такова, что выполнено тождество:
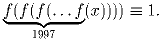
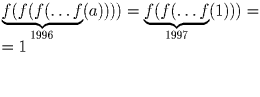 , поэтому
, поэтому
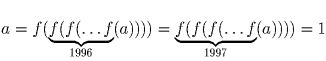 . Итак, f(1) = 1. Кроме единицы существует по
крайней мере ещё одно число x0 такое, что f(x0) = 1 (иначе
. Итак, f(1) = 1. Кроме единицы существует по
крайней мере ещё одно число x0 такое, что f(x0) = 1 (иначе 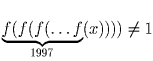 для всех x ≠ 1),
значит, уравнение f(x) = 1 имеет по крайней мере два корня – 1 и
x0. Функция f, равная 1 в точках 1 и 0 и тождественно равная
нулю во всех остальных, показывает, что трёх корней у уравнения может
и не оказаться.
Задача 2:
для всех x ≠ 1),
значит, уравнение f(x) = 1 имеет по крайней мере два корня – 1 и
x0. Функция f, равная 1 в точках 1 и 0 и тождественно равная
нулю во всех остальных, показывает, что трёх корней у уравнения может
и не оказаться.
Задача 2: Рассматриваются все натуральные числа n такие, что числа n + 1 и 2n + 1 – точные квадраты. Найдите наибольший общий делитель всех рассматриваемых чисел.
Решение: n – чётно, иначе 2n + 1 = 4k + 3 не является точным квадратом. Тогда n + 1 = (2l + 1)² для некоторого натурального l, откуда n = 4l(l + 1), и n делится на 8. Кроме того, n делится на 3, иначе одно из чисел n + 1 или 2n + 1 при делении на 3 даст остаток 2 и не сможет быть точным квадратом. Итак, n делится на 24. Так как само число 24 входит в рассматриваемое множество, наибольший общий делитель всех чисел равен 24. Задача 3:Пусть A1A2 … A105 – правильный 105-угольник,
O – центр вписанной в него окружности. Рассматриваются
все вектора 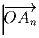 , где номер вершины
n взаимно прост с числом 105 (натуральные числа называются взаимно
простыми, если они не имеют общих делителей, отличных от 1).
Найдите сумму всех рассматриваемых векторов.
, где номер вершины
n взаимно прост с числом 105 (натуральные числа называются взаимно
простыми, если они не имеют общих делителей, отличных от 1).
Найдите сумму всех рассматриваемых векторов.
((Предложена Стасом Васильевым.))
Решение: Прежде всего заметим, что сумма всех векторов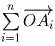 равна 0.
В самом деле, пусть
равна 0.
В самом деле, пусть  . Повернём все векторы на угол
. Повернём все векторы на угол  .
Тогда вектор
.
Тогда вектор 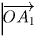 перейдет в
перейдет в
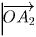 , и т.д. В результате сумма всех векторов
перейдёт в себя. Но единственный вектор не меняющийся при повороте
на угол не кратный 2 π – это нулевой вектор.
, и т.д. В результате сумма всех векторов
перейдёт в себя. Но единственный вектор не меняющийся при повороте
на угол не кратный 2 π – это нулевой вектор.Пусть k – делитель 105 и Sk – сумма всех векторов,
номер которых делится на k. Как и выше, при k ≠ 105 все
эти суммы равны нулевому вектору. Пусть 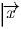 сумма
всех векторов с номерами взаимно простыми с числом 105.
Тогда
сумма
всех векторов с номерами взаимно простыми с числом 105.
Тогда 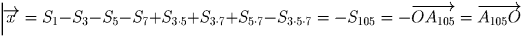 .
.
Торт имеет форму произвольного треугольника. Двое сластен делят его следующим образом. Первый указывает на торте точку, второй проводит через эту точку прямолинейный разрез и забирает себе большую часть. Какую наибольшую часть торта может обеспечить себе первый сластена? Считается, что торт всюду имеет одинаковую толщину.
((Предложена В.Т.Шевалдиным.))
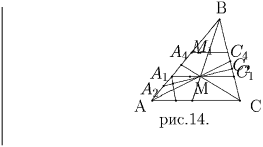
Решение: Пусть ABC – треугольник, который изображает торт (см. рис.14.) и M – точка пересечения его медиан. Покажем, что если первый сластена выберет точку M, то он гарантирует себе 4/9 торта.Действительно, пусть A1C1 || AC и M ∈ A1C1. Тогда из подобия
треугольников ∆ ABC и ∆ A1BC1 имеем
A1B = ⅔AB, C1B = ⅔CB. Следовательно,
 . Пусть
A2C2 не параллелен AC и M ∈ A2C2. Проведем A1A3 || BC.
Тогда
. Пусть
A2C2 не параллелен AC и M ∈ A2C2. Проведем A1A3 || BC.
Тогда 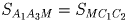 . Значит, при любом повороте отрезка
A1C1 доля первого сластены увеличивается.
. Значит, при любом повороте отрезка
A1C1 доля первого сластены увеличивается.
=0.5mm em:linewidth 0.4pt 0.4pt
Покажем, что при выборе первым сластеной любой другой ≠ M
точки M1 внутри треугольника ∆ ABC второй сластена
может провести разрез так, что доля первого будет меньше
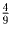 . Действительно, три треугольника,
отсекаемые от ∆ ABC прямыми, параллельными сторонам
этого треугольника и проходящими через точку M,
покрывают ∆ ABC. Поэтому точка M1
в одном из них, без ограничения общности в ∆ A1BC1.
Тогда второй сластена проводит отрезок A4C4 || A1C1,
и доля первого меньше
. Действительно, три треугольника,
отсекаемые от ∆ ABC прямыми, параллельными сторонам
этого треугольника и проходящими через точку M,
покрывают ∆ ABC. Поэтому точка M1
в одном из них, без ограничения общности в ∆ A1BC1.
Тогда второй сластена проводит отрезок A4C4 || A1C1,
и доля первого меньше 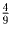 .
.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 10 класс >> 2-й день | Убрать решения |