Задача 1: Натуральные числа t, m и простое число q
удовлетворяют уравнению qt = 2m + 1. Найдите все значения, которые может
принимать число t.
Задача 2: Пять последовательных членов возрастающей арифметической
прогрессии являются простыми натуральными числами. Каким наименьшим
числом может быть разность этой прогрессии?
Задача 3: Петя и Коля играют в «морской бой" на доске размера 1 × 1000
клеток. Флот Пети состоит из 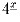 одно-,
одно-,
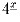 двух-,
двух-, 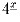 трёх- и
трёх- и
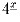 четырёхпалубных кораблей (n-палубный корабль
представляет собой прямоугольник размера 1 × n клеток). Флот
Коли составляют 8 одно- и 8 четырёхпалубных кораблей. По условиям
игры корабли можно располагать только в возрастающем порядке (т.е.
слева от любого корабля стоят корабли только меньшей или равной с ним
палубности), и между любыми двумя кораблями должна находиться хотя бы
одна свободная клетка. Петя убеждён, что его флот может быть
расставлен большим числом способов, чем флот Коли. Прав ли он?
четырёхпалубных кораблей (n-палубный корабль
представляет собой прямоугольник размера 1 × n клеток). Флот
Коли составляют 8 одно- и 8 четырёхпалубных кораблей. По условиям
игры корабли можно располагать только в возрастающем порядке (т.е.
слева от любого корабля стоят корабли только меньшей или равной с ним
палубности), и между любыми двумя кораблями должна находиться хотя бы
одна свободная клетка. Петя убеждён, что его флот может быть
расставлен большим числом способов, чем флот Коли. Прав ли он?
((Предложена С.Э.Нохриным.))
Задача 4: Пусть ABCD – произвольная треугольная пирамида, точка O
принадлежит ей. Соединив точку O со всеми вершинами пирамиды
мы получим четыре пирамиды ABCO, ABOD, AOCD, OBCD.
Определить геометрическое место точек O, для которых сумма
объемов двух каких-либо пирамид из указанных четырех равна
сумме объемов двух оставшихся, если точка O лежит
а) на ребре; б) на грани; в) внутри пирамиды ABCD.
((Предложена В.И.Зенковым.))


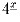 одно-,
одно-,
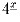 двух-,
двух-, 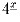 трёх- и
трёх- и
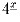 четырёхпалубных кораблей (n-палубный корабль
представляет собой прямоугольник размера 1 × n клеток). Флот
Коли составляют 8 одно- и 8 четырёхпалубных кораблей. По условиям
игры корабли можно располагать только в возрастающем порядке (т.е.
слева от любого корабля стоят корабли только меньшей или равной с ним
палубности), и между любыми двумя кораблями должна находиться хотя бы
одна свободная клетка. Петя убеждён, что его флот может быть
расставлен большим числом способов, чем флот Коли. Прав ли он?
четырёхпалубных кораблей (n-палубный корабль
представляет собой прямоугольник размера 1 × n клеток). Флот
Коли составляют 8 одно- и 8 четырёхпалубных кораблей. По условиям
игры корабли можно располагать только в возрастающем порядке (т.е.
слева от любого корабля стоят корабли только меньшей или равной с ним
палубности), и между любыми двумя кораблями должна находиться хотя бы
одна свободная клетка. Петя убеждён, что его флот может быть
расставлен большим числом способов, чем флот Коли. Прав ли он?