 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 11 класс. 2-й день |
|
|
Натуральные числа t, m и простое число q удовлетворяют уравнению qt = 2m + 1. Найдите все значения, которые может принимать число t.
Решение: Перепишем уравнение в виде qt – 1 = 2m. Значит, q – нечетное число. Так как для t > 1 qt – 1 = (q – 1)(qt – 1 + qt – 2 + … + 1), то при нечетном t сумма qt – 1 + qt – 2 + … + 1 нечетна и больше 1. Следовательно, в этом случае уравнение решений не имеет. При t = 1 уравнение имеет решение, например, q = 3, m = 1 или q = 5, m = 2. Пусть теперь t – четно и равно 2k. В этом случае q2k – 1 = (qk – 1)(qk + 1) = 2m. Но тогда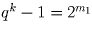 , а
, а 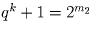 , где m1 + m2 = m. Так
как
, где m1 + m2 = m. Так
как 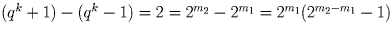 ,
то
,
то 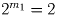 , а
, а 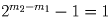 . Отсюда m1 = 1, m2 – m1 = 1.
Поэтому m2 = 2, а m = 3. Из уравнения qk – 1 = 2 имеем k = 1 и
q = 3. Таким образом, имеем решение t = 2,q = 3,m = 3.
. Отсюда m1 = 1, m2 – m1 = 1.
Поэтому m2 = 2, а m = 3. Из уравнения qk – 1 = 2 имеем k = 1 и
q = 3. Таким образом, имеем решение t = 2,q = 3,m = 3.Ответ: t = 1 или t = 2.
Задача 2:
Пять последовательных членов возрастающей арифметической прогрессии являются простыми натуральными числами. Каким наименьшим числом может быть разность этой прогрессии?
Решение: Пусть a – первый член, а d > 0 – разность данной прогрессии. d не может быть нечётным числом, так как иначе среди членов прогрессии будет не менее двух чётных чисел. Кроме того, она делится на 3. Действительно, в противном случае как среди чисел a, a + d, a + 2d, так и среди чисел a + 2d, a + 3d, a + 4d найдутся делящиеся на 3. Откуда a + 2d = 3, а так как d > 1, то a < 0. Противоречие. Значит, d делится на 6, и поэтому d ≥ 6. Пример такой прогрессии с d = 6: 5, 11, 17, 23, 29. Задача 3:
Петя и Коля играют в «морской бой" на доске размера 1 × 1000
клеток. Флот Пети состоит из 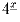 одно-,
одно-,
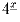 двух-,
двух-, 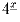 трёх- и
трёх- и
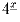 четырёхпалубных кораблей (n-палубный корабль
представляет собой прямоугольник размера 1 × n клеток). Флот
Коли составляют 8 одно- и 8 четырёхпалубных кораблей. По условиям
игры корабли можно располагать только в возрастающем порядке (т.е.
слева от любого корабля стоят корабли только меньшей или равной с ним
палубности), и между любыми двумя кораблями должна находиться хотя бы
одна свободная клетка. Петя убеждён, что его флот может быть
расставлен большим числом способов, чем флот Коли. Прав ли он?
четырёхпалубных кораблей (n-палубный корабль
представляет собой прямоугольник размера 1 × n клеток). Флот
Коли составляют 8 одно- и 8 четырёхпалубных кораблей. По условиям
игры корабли можно располагать только в возрастающем порядке (т.е.
слева от любого корабля стоят корабли только меньшей или равной с ним
палубности), и между любыми двумя кораблями должна находиться хотя бы
одна свободная клетка. Петя убеждён, что его флот может быть
расставлен большим числом способов, чем флот Коли. Прав ли он?
((Предложена С.Э.Нохриным.))
Решение: Петя не прав. Оба флота можно расставить одним и тем же числом способов. Действительно, так как корабли располагаются в возрастающем порядке, то расположение флота любого из игроков однозначно определяется количеством свободных клеток между кораблями и количеством свободных клеток до первого и после последнего корабля. У Пети и Коли одинаковое число кораблей и они имеют одинаковое число свободных клеток 1000 – 40 = 960 при любой расстановке кораблей. Таким образом число расстановок обоих флотов равно числу разбиений 960 на 17 слагаемых, из которых все кроме возможно первого и последнего не равны нулю. Задача 4:Пусть ABCD – произвольная треугольная пирамида, точка O принадлежит ей. Соединив точку O со всеми вершинами пирамиды мы получим четыре пирамиды ABCO, ABOD, AOCD, OBCD. Определить геометрическое место точек O, для которых сумма объемов двух каких-либо пирамид из указанных четырех равна сумме объемов двух оставшихся, если точка O лежит а) на ребре; б) на грани; в) внутри пирамиды ABCD.
((Предложена В.И.Зенковым.))
Решение:Случай а):
Пусть ABCD – искомая пирамида.
Если точка O лежит на ребре, скажем, AD (см. рис. а.), то объемы
двух из четырех рассматриваемых пирамид равны нулю. Следовательно,
VABCO = VBCDO и так как VABCO + VBCDO = VABCD, то
VABCO = ½VABCD.
Поскольку VABCO = ⅓SABCh1, где
h1 – высота ABCO, опущенная из вершины O на основание ABC,
а VABCD = ⅓SABCh, где
h – высота ABCD, опущенная из вершины D на основание ABC,
то 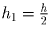 и в этом случае точка O
лежит на середине ребра AD.
Таким образом в случае а) геометрическое место точек O состоит из
шести точек, лежащих на серединах ребер пирамиды ABCD.
и в этом случае точка O
лежит на середине ребра AD.
Таким образом в случае а) геометрическое место точек O состоит из
шести точек, лежащих на серединах ребер пирамиды ABCD.
Случай б). Пусть O лежит на грани ABC (см. рис.б.).
Тогда пирамида ABCD разбивается
на 3 пирамиды с объемами V1, V2 и V3 такими, что V1 = V2 + V3 = ½VABCD.
А так как высота, опущенная из точки D у этих пирамид одна и та же, то
это равенство можно записать как S1 = S2 + S3 = ½S ∆ ABC,
где Si – площадь оснований пирамид на грани ABC. Легко доказать тогда,
что O лежит на одной из трех средних линий ∆ ABC
(пусть S1 = S ∆ OAB, тогда
S ∆ OAB = ½S ∆ ABC  O лежит на средней линии || AB).
В силу произвольности выбора грани ABC, получаем, что в случае б)
геометрическое место точек O состоит из 12 средних линий 4–х граней
пирамиды ABCD.
O лежит на средней линии || AB).
В силу произвольности выбора грани ABC, получаем, что в случае б)
геометрическое место точек O состоит из 12 средних линий 4–х граней
пирамиды ABCD.
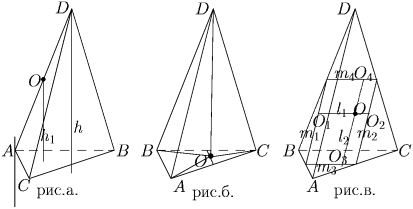
Случай в). Пусть O – внутренняя точка пирамиды ABCD и пусть
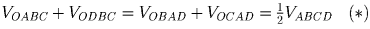 (см. рис.13.в.). Все точки плоскости p1, проходящей через точку
O и параллельной грани ABC, равноудалены от грани ABC.
Аналогично, все точки плоскости p2, проходящей через точку O и
параллельной грани DBC, равноудалены от грани DBC. Тогда p1 и
p2 пересекаются по прямой l1 || BC (т.к. BC || p1 и
BC || p2), для любой точки O′ которой
VO′ABC + VO′DBC = const, а значит (*) выполняется. l1
пересекает грани BAD и CAD в точках O1 и O2,
соответственно. Но в точке O1
(см. рис.13.в.). Все точки плоскости p1, проходящей через точку
O и параллельной грани ABC, равноудалены от грани ABC.
Аналогично, все точки плоскости p2, проходящей через точку O и
параллельной грани DBC, равноудалены от грани DBC. Тогда p1 и
p2 пересекаются по прямой l1 || BC (т.к. BC || p1 и
BC || p2), для любой точки O′ которой
VO′ABC + VO′DBC = const, а значит (*) выполняется. l1
пересекает грани BAD и CAD в точках O1 и O2,
соответственно. Но в точке O1 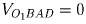 и следовательно по
пункту б) O1 лежит на одной из трех средних линий ∆ BAD,
а именно на средней линии m1 || AD (т.к. из (*)
и следовательно по
пункту б) O1 лежит на одной из трех средних линий ∆ BAD,
а именно на средней линии m1 || AD (т.к. из (*)
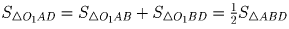 ). Аналогично
доказывается, что O2 лежит на средней линии ∆ ADC m2 || AD. Проведя аналогичные рассуждения (через O проводим
плоскости параллельные граням BAD и CAD) получаем, что O лежит
прямой l2 || AD, на которой выполняется (*) и которая
пересекает грани ABC и DBC в точках O3 и O4,
соответственно, причем O3 и O4 лежат на средних линиях этих
граней m3 и m4, параллельных BC. Отсюда, l1 и l2 (а
значит и точка O) лежат в плоскости, проходящей через m1, m2,
m3, m4 (т.к. O1, O2 и O3, O4 лежат в этой
плоскости). Обозначим сечение этой плоскости и пирамиды ABCD через
q. Для любой точки сечения q выполняется (*). Действительно,
через любую точку сечения q можно провести прямую
). Аналогично
доказывается, что O2 лежит на средней линии ∆ ADC m2 || AD. Проведя аналогичные рассуждения (через O проводим
плоскости параллельные граням BAD и CAD) получаем, что O лежит
прямой l2 || AD, на которой выполняется (*) и которая
пересекает грани ABC и DBC в точках O3 и O4,
соответственно, причем O3 и O4 лежат на средних линиях этих
граней m3 и m4, параллельных BC. Отсюда, l1 и l2 (а
значит и точка O) лежат в плоскости, проходящей через m1, m2,
m3, m4 (т.к. O1, O2 и O3, O4 лежат в этой
плоскости). Обозначим сечение этой плоскости и пирамиды ABCD через
q. Для любой точки сечения q выполняется (*). Действительно,
через любую точку сечения q можно провести прямую 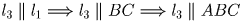 и l3 || BCD. Тогда для любой точки O′ на l3 имеем
VO′ABC + VO′DBC = const, но l3 пересекает l2
и l3 || BCD. Тогда для любой точки O′ на l3 имеем
VO′ABC + VO′DBC = const, но l3 пересекает l2
 const = ½VABCD. Равенство (*) можно
записать 3 различными способами (
const = ½VABCD. Равенство (*) можно
записать 3 различными способами (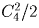 ), поэтому в случае в)
искомое геометрическое место точек это 3 сечения пирамиды ABCD
плоскостями параллельными (BC и AD), (AB и CD), (AC и
BD), соответственно и проходящими через середины 4–х оставшихся
ребер.
), поэтому в случае в)
искомое геометрическое место точек это 3 сечения пирамиды ABCD
плоскостями параллельными (BC и AD), (AB и CD), (AC и
BD), соответственно и проходящими через середины 4–х оставшихся
ребер.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 11 класс >> 2-й день | Убрать решения |