 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 7 класс >> 2-й день | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 7 класс. 2-й день |
|
|
Из чисел 1,2, … ,100 выбрано 51 число. Докажите, что среди выбранных чисел найдется два, одно из которых делится на другое. Можно ли уменьшить число выбранных чисел с сохранением указанного свойства?
(Математический фольклор.)
Решение:первый способ. Разобьём выбранные числа на два множества: m чисел в множестве A – это все числа не превосходящие 50 и n чисел в множестве B – это все числа большие 50. Так как n ≤ 50, а всего чисел 51, то m ≥ 1. Аналогично доказывается, что n ≥ 1, то есть оба множества не пусты. Каждому числу из множества A поставим в соответствие число из множества 51,52, … ,100 следующим образом: для любого числа a из A найдётся такое число k, что k • a лежит в множестве чисел 50,51, … ,100. Действительно,

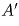 , лежащее в
множестве чисел 51,52, … ,100.
При этом возможны два случая.
, лежащее в
множестве чисел 51,52, … ,100.
При этом возможны два случая.1. Все числа из множества 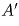 попарно различны.
Тогда, так как множество B так же содержится в множестве
51,52, … ,100, состоящем из 50 чисел, а m + n = 51, то
существуют по крайне мере такие два числа
a из A и b из B, что k • a = b
(где k – число, которое использовалось при отображении числа a
на множество
попарно различны.
Тогда, так как множество B так же содержится в множестве
51,52, … ,100, состоящем из 50 чисел, а m + n = 51, то
существуют по крайне мере такие два числа
a из A и b из B, что k • a = b
(где k – число, которое использовалось при отображении числа a
на множество 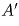 )
)
2. В множестве 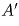 есть два совпадающих числа.
То есть существуют числа a1 и a2 из A такие, что
2c • a1 = 2d • a2. Без ограничения общности можно считать,
что c < d, а значит a1 = 2d – c • a2, что и требовалось доказать.
есть два совпадающих числа.
То есть существуют числа a1 и a2 из A такие, что
2c • a1 = 2d • a2. Без ограничения общности можно считать,
что c < d, а значит a1 = 2d – c • a2, что и требовалось доказать.
Уменьшить число выбранных чисел с сохранением указанного свойства нельзя. Пример: выбранные числа 51,52, … ,100
второй способ. Разобьём все числа первой сотни на 50 групп: первая – 1, 2, 4, 8, 16, 32, 64, вторая – 3, 6, 12, 24, 48, 96, третья – 5, 10, 20, 40, 80, и.т.д.(первое число каждой группы нечётное, а следующее в 2 раза больше предыдущего). По принципу Дирихле среди выбранных чисел хотя бы два попадут в одну группу. Они, очевидно, искомые. Уменьшить число выбранных чисел нельзя; достаточно рассмотреть набор из всех чисел, больших 50.
Задача 2:
Пешеход идет со скоростью 5 км/ч по шоссе, по которому в оба направления курсируют рейсовые автобусы, встречающиеся между собой каждые 5 минут. В 10 часов пешеход заметил, что рядом с ним повстречались автобусы, и через 2 часа он был в точке, где также повстречались автобусы. За это время он считал встречные и обгоняющие его автобусы, и оказалось, что встречных было на 4 больше. Определите скорость автобусов.
((Предложена Е.С.Зенковой.))
Решение: Первый способ. Пусть V – скорость автобусов, S – расстояние между соседними автобусами, идущими в одну сторону. Тогда (так как два встречных автобуса, находящиеся на расстоянии S встречаются
через
(так как два встречных автобуса, находящиеся на расстоянии S встречаются
через 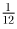 часа).
часа).Движение относительно. Рассмотрим задачу, считая что пешеход неподвижен.
Тогда шоссе движется относительно пешехода со скоростью 5 км/ч,
встречные автобусы движутся относительно пешехода со скоростью (V + 5) км/ч,
а обгоняющие его автобусы – со скоростью (V – 5) км/ч.
За 2 часа число встречных автобусов 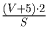 ,
а число обогнавших пешехода автобусов
,
а число обогнавших пешехода автобусов 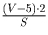 .
Имеем уравнение
.
Имеем уравнение 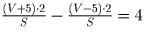 ,
подставляя в которое значение
,
подставляя в которое значение  и решая относительно V, находим, что V = 30 км/ч.
и решая относительно V, находим, что V = 30 км/ч.
Второй способ.
Пусть V – скорость автобусов,
 – расстояние между соседними автобусами,
идущими в одну сторону (см. 1-ое решение),
k – число встречных автобусов,
m – число обогнавших пешехода автобусов,
A – точка, где находился пешеход в 10 часов,
B – точка, где находился пешеход в 12 часов.
Расстояние AB = 5 • 2 = 10 км.
– расстояние между соседними автобусами,
идущими в одну сторону (см. 1-ое решение),
k – число встречных автобусов,
m – число обогнавших пешехода автобусов,
A – точка, где находился пешеход в 10 часов,
B – точка, где находился пешеход в 12 часов.
Расстояние AB = 5 • 2 = 10 км.
В 12 часов первый встречный автобус находился от точки B на расстоянии
S • k (обозначим эту точку M),
а первый обогнавший пешехода автобус находился от точки B
на расстоянии S • m (обозначим эту точку N).
Но оба эти автобуса в 10 часов начали движение из точки A,
значит A – середина отрезка MN. Имеем уравнение
S • k – 10 = S • m + 10, подставляя в которое
 и k – m = 4 и решая относительно V, находим,
что V = 30 км/ч.
и k – m = 4 и решая относительно V, находим,
что V = 30 км/ч.
Третий способ.
Пусть V – скорость автобусов,  – расстояни
между соседними автобусами, идущими в одну сторону (см. 1-ое решение),
A – точка, где находился пешеход в 10 часов,
B – точка, где находился пешеход в 12 часов. AB = 5 • 2 = 10 км.
– расстояни
между соседними автобусами, идущими в одну сторону (см. 1-ое решение),
A – точка, где находился пешеход в 10 часов,
B – точка, где находился пешеход в 12 часов. AB = 5 • 2 = 10 км.
За 10 мин автобус проходит отрезок длины S, то есть в точку A через каждые 10 мин приходит следующий автобус. Следовательно, к 12 часам в точке A будут находится 12 встречный и 12 обогнавший пешехода автобусы. Однако в 12 часов в точке B также встретились 2 автобуса, а значит на отрезке AB укладывается целое число отрезков длины S (обозначим его через k).
Если бы пешеход 2 часа простоял в точке A, то мимо него в обе стороны прошло равное число автобусов – 12. Мгновенно переместим пешехода в 12 часов из точки A в точку B получаем, что число встречных автобусов равно 12 + k, а число обогнавших пешехода автобусов равно 12 – k.
(12 + k) – (12 – k) = 4, откуда k = 2.
S • k = 10, откуда S = 5 км.
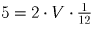 , откуда V = 30 км/ч.
, откуда V = 30 км/ч.
(Рекомендована жюри Российской олимпиады.) У трёх братьев – Андрея, Василия и Сергея – дни рождения совпадают. Когда старшему из них, Андрею, исполнилось 12 лет, то оказалось, что сумма возрастов всех братьев делится на 12. То же случилось, когда 12 лет исполнилось Василию. Докажите, что тоже самое случится, когда 12 лет исполнится Сергею.
(Рекомендована жюри Российской олимпиады.)
Решение: Пусть, когда Андрею исполнилось 12 лет, Сергею было x лет, а Василию – y лет. Так как 12 + x + y делится на 12 и x < y < 12, то x + y = 12. Василию исполнилось 12 лет через 12 – y = x лет, когда Сергею исполнилось 2x. 2x + 12 + (12 + x) делится на 12. Значит 3x делится на 12. Откуда x = 4, а y = 8. Сергею исполнится 12 лет через 12 – x = 8 лет, когда Василию будет y + 8 = 16, а Андрею 20. 12 + 16 + 20 делится на 12, что и требовалось доказать.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 7 класс >> 2-й день | Убрать решения |