 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 9 класс >> 1-й день | Показать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 9 класс. 1-й день |
|
|
Даны корни x0 и x1, x0 и x2, … , x0 и xn квадратных трехчленов y = x² + \ + a1x + b1, y = x² + a2x + b2, … , y = x² + anx + bn. Найдите корни квадратного трехчлена
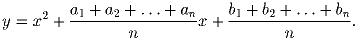
(Рекомендована жюри Российской олимпиады.)
Задача 2:Сколько существует пар (x,y) целых чисел x и y, заключённых между 1 и 1000, и таких, что x² + y² делится на 49? Пары (x,y) и (y,x) при x ≠ y считаются различными.
(Предложена Е.С.Зенковой.)
Задача 3:На плоскости заданы точки A1,A2,A3, … ,A1999 так, что A1A2 = 10,A1A3 = 5, A2A3 = \ = 7, а для всех натуральных чисел N, больших 3, AN – середина отрезка AN – 3AN – 2.
а) Найдите площадь треугольника A1997A1998A1999.
б) Какой из углов треугольника A1997A1998A1999 является наибольшим?
(Предложена Д.О.Филимоненковым.)
Задача 4: В восьми вазах лежат конфеты: в первой – 1, во второй – 2, в третий – 3, , в восьмой – 8 конфет. Маша съедает каждый день ровно k конфет (k – натуральное число), причём из каждой вазы берёт не более одной конфеты. Найдите все значения k, при которых Маша сможет съесть все конфеты.((Предложена С.Э.Нохриным.))
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 9 класс >> 1-й день | Показать решения |