 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Областной тур. 9 класс. 1-й день |
|
|
Даны корни x0 и x1, x0 и x2, … , x0 и xn квадратных трехчленов y = x² + \ + a1x + b1, y = x² + a2x + b2, … , y = x² + anx + bn. Найдите корни квадратного трехчлена
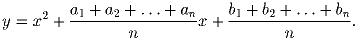
(Рекомендована жюри Российской олимпиады.)
Решение: Так как исследуемый трёхчлен есть среднее арифметическое трёхчленов с корнями x0 и x1, x0 и x2, … , x0 и xn, число x0 является его корнем. Второй корень, равный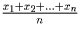 ,
находится по теореме Виета.
Задача 2:
,
находится по теореме Виета.
Задача 2: Сколько существует пар (x,y) целых чисел x и y, заключённых между 1 и 1000, и таких, что x² + y² делится на 49? Пары (x,y) и (y,x) при x ≠ y считаются различными.
(Предложена Е.С.Зенковой.)
Решение: Рассмотрев всевозможные остатки от деления чисел x и y на 7, убеждаемся, что x² + y² делится на 49 тогда и только тогда, когда и x и y делятся на 7. Всего существует 142 натуральных числа, делящихся на 7 и не превосходящих 1000, а поэтому таких пар 142².Задача 3:
На плоскости заданы точки A1,A2,A3, … ,A1999 так, что A1A2 = 10,A1A3 = 5, A2A3 = \ = 7, а для всех натуральных чисел N, больших 3, AN – середина отрезка AN – 3AN – 2.
а) Найдите площадь треугольника A1997A1998A1999.
б) Какой из углов треугольника A1997A1998A1999 является наибольшим?
(Предложена Д.О.Филимоненковым.)
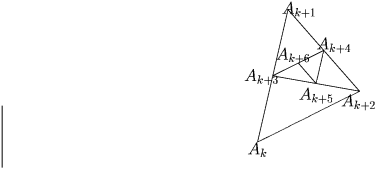
Решение: Заметим (см. рисунок), что для любого k треугольники AkAk + 1Ak + 2 и Ak + 4Ak + 5Ak + 6 подобны с коэффициентом 4. Имеем
((Предложена С.Э.Нохриным.))
Решение: Число дней, за которе Маша сможет съесть все конфеты не менее 8 (иначе не опустошить восьмую вазу), общее число конфет – 36, поэтому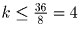 . Для того, чтобы показать, что все такие k
удовлетворяют условию задачи, распределим вазы в k групп так, чтобы
конфет в каждой группе было поровну. Алгоритм поедания конфет таков:
каждый день съедается по одной конфете из каждой группы (неважно из
какой вазы). Искомое распределение:
. Для того, чтобы показать, что все такие k
удовлетворяют условию задачи, распределим вазы в k групп так, чтобы
конфет в каждой группе было поровну. Алгоритм поедания конфет таков:
каждый день съедается по одной конфете из каждой группы (неважно из
какой вазы). Искомое распределение:при k = 4: 1-ая + 8-ая вазы, 2-ая + 7-ая вазы, 3-я + 6-ая вазы, и 4-ая + 5-ая вазы.
при k = 3: 1-ая + 2-ая + 3-я + 6-ая вазы, 4-я + 8-ая вазы, и 7-ая + 5-ая вазы.
при k = 2: 1-ая + 8-ая + 2-ая + 7-ая вазы и 3-я + 6-ая + 4-ая + 5-ая вазы.
при k = 1 единственная группа состоит из всех ваз.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |