 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Районный тур >> 9 класс | Убрать решения |
|
|
| XXXVII Екатеринбургская городская олимпиада, 1996-1997. Районный тур. 9 класс |
|
|
Решение: Так как (x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 3x² – 2(a + b + c) + ab + bc + ca, данное уравнение – квадратное, и для доказательства достаточно показать неотрицательность его дискриминанта, который, очевидно, равен 4a² + 4b² + 4c² – 4(ab + bc + ca). Это осуществляется сложением очевидных неравенств a² + b² ≥ 2ab, b² + c² ≥ 2bc, и c² + a² ≥ ≥ 2ca.
Задача 2: Пусть x, y и z – натуральные числа. Доказать, что если x² + + y² = z², то 3 делит x или 3 делит y.
Решение: Допустим, что ни x, ни y не делится на 3. Заметим, что любое число t, не делящееся на 3, записывается в виде t = 3k + 1, или t = 3k + 2, и поэтому t² = 3m + 1. Следовательно, левая часть при делении на 3 дает остаток 2, а правая часть при делении на 3 дает остаток 1. Противоречие.
Задача 3: Окружность окрашена в два разных цвета. Доказать, что найдется равнобедренный треугольник c одноцветными вершинами.
Решение: Рассмотрим произвольный правильный пятиугольник, вписанный в окружность. Среди его вершин найдутся три, окрашенные одинаково (принцип Дирихле). Треугольник с вершинами в этих точках равнобедренный, так как он составлен либо из двух сторон и диагонали, либо из двух диагоналей и стороны рассмотренного правильного пятиугольника. Этот треугольник, очевидно, искомый.
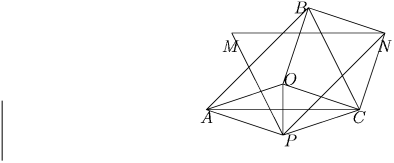
Задача 4: Точки M, N и P симметричны центру описанной вокруг треугольника ABC окружности относительно сторон AB, BC и CA. Доказать, что треугольники ABC и MNP равны.
Решение: Рассмотрим треугольники ABC и MNP (см. рис.2). Пусть точка O – центр описанной окружности. Тогда AOCP – ромб и OCNB – ромб. Следовательно, отрезки AP, OC и BN, параллельны и равны, поэтому четырехугольник APNB – параллелограмм. Тогда AB = PN. Аналогично AC = MN, и BC = MP. Поэтому треугольники ABC и MNP равны по трем сторонам.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVII олимпиада, 1996-1997 >> Районный тур >> 9 класс | Убрать решения |