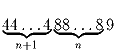
Задача 1: Доказать, что число является точным квадратом для любого натурального числа n.

Задача 2: Верно ли, что для любых натуральных чисел A, B и C найдется натуральное число K такое, что A + K делится на C, а A + B + K делится на C + 1?

Задача 3: В городе n домов. Какое максимальное число непересекающихся заборов можно построить в этом городе, если каждый забор огораживает хотя бы один дом и никакие два забора не огораживают одну и ту же совокупность домов?

Задача 4: Докажите равенство треугольников по трем медианам.