 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 10 класс >> 1-й день | Показать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 10 класс. 1-й день |
|
|
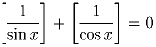
(Н.Агаханов)
Задача 2: Дана последовательность a1,a2,a3, … , где an = n² + n + 1 при любом n ≥ 1. Докажите, что произведение любых двух соседних членов этой последовательности также является её членом.
(С.Токарев)
Задача 3: В треугольнике ABC проведена биссектриса внешнего угла A (см. рис.17), которая пересекает продолжение стороны BC в точке D. Докажите, что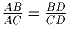 .
Задача 4:
На круговой автостраде ровно 1998 светофоров. Каждую минуту они
одновременно меняют цвет по следующему правилу:
.
Задача 4:
На круговой автостраде ровно 1998 светофоров. Каждую минуту они
одновременно меняют цвет по следующему правилу:Каждый светофор меняет цвет в зависимости от цвета двух соседних (справа и слева), причём
1) если два соседних светофора горели одним цветом, то светофор между ними загорается этим же цветом.
2) если два соседних светофора горели разными цветами, то светофор между ними загорается третьим цветом.
В начальный момент все светофоры кроме одного были зеленые, а один — красный. Верно ли, что через какое-то время все светофоры будут гореть жёлтым цветом? Ответ обосновать.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 10 класс >> 1-й день | Показать решения |