 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 11 класс >> 1-й день | Показать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 11 класс. 1-й день |
|
|
Найти наибольшее значение a² + b² + c², если |ax² + bx + c| ≤ 1 для всех x ∈ [ – 1,\,1].
Задача 2: Найдите два многочлена P(x) и Q(x) с целыми коэффициентами таких, что множество значений дробно-рациональной функции
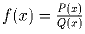 есть промежуток
есть промежуток 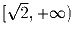 .
.
(В.Сендеров)
Задача 3:На окружности, описанной вокруг треугольника ABC, отмечены точки A1, B1, C1 – середины дуг CAB, ABC и BCA соответственно. Докажите, что касательные к окружности в точках A1 и C1 и серединный перпендикуляр к отрезку BB1 пересекаются в одной точке.
(М.Сонкин)
Задача 4:В некоторой компании у каждых трёх человек имеется ровно один общий знакомый среди членов этой компании. Сколько человек может насчитывать такая компания?
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 11 класс >> 1-й день | Показать решения |