 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |
|
|
| XXXVIII Екатеринбургская городская олимпиада, 1997-1998. Областной тур. 9 класс. 1-й день |
|
|
(Т.Емельянова)
Решение:Не имеет. Действительно, пусть x0 – его целый корень. Тогда x0 < 0. Обозначим k = – x0, тогда – k1997 + 2k1996 – 3k1995 + … – 1997x + 1998 = 0, 2k1996 + 4k1994 + … + 1998 = k1997 + 3k1995 + … + 1997k Теперь если k = 1, то 2k1996 > k1997, 4k1994 > 3k1995, … 1998 > 1997k, и левая часть последнего уравнения больше правой; если же k ≥ 2, то 2k1996 < k1997, 4k1994 < 3k1995, … 1998 < 1997k, и правая часть уравнения больше левой.
Задача 2: Найдите наибольший общий делитель всех чисел вида 2n5 + 1998n, где n = 1,\,2,\,3,\,4,\, … .
Решение:
При n = 1 и n = 2 получаются числа 2000 и 4060, наибольший общий делитель которых – число 20. Значит, наибольший общий делитель всех рассматриваемых чисел есть делитель 20. Покажем, что для всех натуральных n число 2n5 + 1998n делится на 20. Для этого достаточно показать, что всякое число вида n5 – n = ½(2n5 + 1998n) – 1000n делится на 10, что эквивалентно утверждению, что числа n5 и n оканчиваются на одну и ту же цифру. Это проверяется путем рассмотрения всех цифр, на которые может оканчиваться число n.
ОТВЕТ: Наибольший общий делитель равен 20.
Задача 3: Докажите, что отрезок, соединяющий середины противоположных сторон выпуклого четырёхугольника, делит его диагонали в равных отношениях.
(М.Сонкин)
Решение:Пусть M и N – середины сторон AB и DC. Опустим перпендикуляры
из всех вершин на прямую MN: AA1,BB1,CC1 и DD1 (см. рис.15).
Тогда AA1 = BB1, CC1 = DD1, из подобия треугольников AA1E и
CC1E имеем 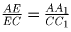 , а из подобия треугольников
BB1F и DD1F имеем
, а из подобия треугольников
BB1F и DD1F имеем 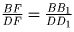 . Из полученных
уравнений немедленно следует утверждение задачи, так как AA1 = BB1,
и CC1 = DD1.
. Из полученных
уравнений немедленно следует утверждение задачи, так как AA1 = BB1,
и CC1 = DD1.
Задача 4: На доске 5 × 5 16 полей заняты королями. Докажите, что найдётся квадрат размером 2 × 2, в клетках которого будет не менее трёх королей.
Решение:
Предположим, что нам удалось расставить королей так, что в каждом квадрате 2 × 2 нет трёх королей. Тогда в верхнем левом угловом квадрате 4 × 4 расположено не более 8 королей, поэтому в заштрихованных клетках (см. рис.16.) их не менее 8, причём в трёх помеченными нуликами клеток расположено не более 2 королей. Тогда в заштрихованных клетках ровно 8 королей, в клетках, помеченных крестиками, королей нет, а значит, в верхнем левом угловом квадрате 3 × 3 расположены оставшиеся 8 королей. Выберем в этом квадрате произвольно квадрат 2 × 2. В нём не более одной свободной клетки – противоречие.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXVIII олимпиада, 1997-1998 >> Областной тур >> 9 класс >> 1-й день | Убрать решения |