Задача 1: Доказать, что

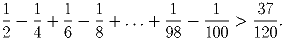
Задача 2: Точка B лежит на отрезке AC; AB = 2, BC = 1.

Указать на прямой AB все точки M, для которых AM + MB = CM.

Задача 3: В классе 30 человек. Только двое из них не любят ни математику, ни физику, ни биологию. 14 учеников любят математику, 15 – физику, 11 – биологию, 6 – физику и математику, 5 –физику и биологию и 3 – математику и биологию.

Сколько учащихся любят сразу 3 указанных предмета?

Задача 4: У продавца имеется 10 гирь весом 1, 2, 3, …10 кг. Известно, что все покупатели, стоящие в очереди к продавцу, купили разное целое число килограммов товара. Какое максимальное число покупателей могло стоять в очереди?