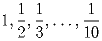Задача 1: Можно ли из 1996 дробей

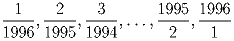
выбрать три, произведение которых равно единице?

Задача 2: Записав числа

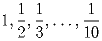
в каком-либо порядке, соедините их знаками « + ",« – ", « × " (умножить), и «:" (разделить) так, чтобы полученное выражение равнялось 0. (Скобки использовать нельзя).

Задача 3: В треугольниках  ∆ ABC и  ∆ A′B′C′ стороны AB, BC, A′B′, B′C′ равны между собой. Треугольник  ∆ A′B′C′ находится внутри  ∆ ABC. Возможно ли такое?

Задача 4: Автомат при опускании гривенника выбрасывает пять«двушек", а при опускании «двушки" – пять гривенников. Может ли Петя, подойдя к автомату с одной «двушкой", получить после нескольких опусканий одинаковое количество «двушек" и гривенников?