Задача 1:

Два игрока играют в следующую игру. Вначале на доске написаны числа 2, 4, 6, 8, …, 1998. За один ход можно уменьшить на 1 любое из написанных чисел. При этом с доски стираются числа, равные нулю, и числа, совпадающие с какими-то из уже написанных на доске чисел. Проигрывает тот, после чьего хода на доске не останется ни одного числа. Кто выигрывает при наилучшей игре с обеих сторон?

Задача 2: На горизонтальной плоскости из трёх точек, отстоящих от точки основания вертикальной башни на расстояние 100, 200 и 300 метров, измерили угол под которым видна башня. Измеренные углы в сумме составляют 90. Можно ли по этой информации определить высоту башни?

Задача 3: Доказать, что для любых действительных чисел x и y найдутся числа a ∈ [0;1] и b ∈ [0;1] такие, что

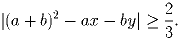
Задача 4: Докажите, что среди любых 39 последовательных натуральных чисел обязательно найдётся такое, сумма цифр которого делится на 11.