 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 11 класс >> 1-й день | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Областной тур. 11 класс. 1-й день |
|
|
Два игрока играют в следующую игру. Вначале на доске написаны числа 2, 4, 6, 8, …, 1998. За один ход можно уменьшить на 1 любое из написанных чисел. При этом с доски стираются числа, равные нулю, и числа, совпадающие с какими-то из уже написанных на доске чисел. Проигрывает тот, после чьего хода на доске не останется ни одного числа. Кто выигрывает при наилучшей игре с обеих сторон?
Решение:
ОТВЕТ: Выиграет первый игрок.
Выигрышная стратегия для первого игрока такова: каждый раз выбирать для своего хода наименьшее из написанных на доске не-чёт-ных чисел, а если таковых нет — произвольное (чётное) число.
Если первый игрок следует своей стратегии, то после первого его хода образуется одно нечётное число, после хода второго игрока — 0 и 2 нечётных. Следовательно, после хода первого вновь будет ровно одно нечётное число.
При этом не может появиться пара (2k – 1,2k), так как она может возникнуть только из пары (2k – 1,2k + 1), а первый игрок выбирает для хода меньшее из двух написанных нечётных чисел. Значит, после хода второго игрока вновь будет 0 или 2 нечётных числа (ровно одно могло бы появиться, если бы перед каждым ходом была пара (2k – 1,2k)) и т.д. Значит, перед каждым ходом первого игрока число нечётных чисел не равно 1 и он не проигрывает.
Задача 2: На горизонтальной плоскости из трёх точек, отстоящих от точки основания вертикальной башни на расстояние 100, 200 и 300 метров, измерили угол под которым видна башня. Измеренные углы в сумме составляют 90. Можно ли по этой информации определить высоту башни? Решение: Пусть высота башни равна H, а углы, под которыми видна башня, равны соответственно α , β и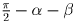 .
Тогда
.
Тогда 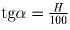 ,
, 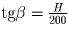 , и
, и
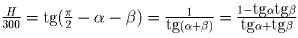 .
Имеем уравнение:
.
Имеем уравнение:
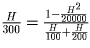 ,
решая которое, находим H = 100м.
ОТВЕТ: Высота башни 100 метров.
Задача 3:
Доказать, что для любых действительных чисел x и y найдутся числа
a ∈ [0;1] и b ∈ [0;1] такие, что
,
решая которое, находим H = 100м.
ОТВЕТ: Высота башни 100 метров.
Задача 3:
Доказать, что для любых действительных чисел x и y найдутся числа
a ∈ [0;1] и b ∈ [0;1] такие, что
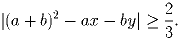
Решение: Предположим противное, т.е., что для некоторых чисел x0 и y0 неравенство
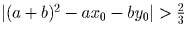 справедливо для
любых чисел a ∈ [0;1] и b ∈ [0;1]. Подставляя вместо a и b
числа 0 и 1, 1 и 0, и, наконец, 1 и 1, получим систему:
справедливо для
любых чисел a ∈ [0;1] и b ∈ [0;1]. Подставляя вместо a и b
числа 0 и 1, 1 и 0, и, наконец, 1 и 1, получим систему: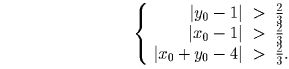
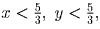 откуда x + y – 4 < – ⅔ — противоречие с третьим неравенством системы.
Задача 4:
Докажите, что среди любых 39 последовательных натуральных чисел
обязательно найдётся такое, сумма цифр которого делится на 11.
откуда x + y – 4 < – ⅔ — противоречие с третьим неравенством системы.
Задача 4:
Докажите, что среди любых 39 последовательных натуральных чисел
обязательно найдётся такое, сумма цифр которого делится на 11.Решение: Обозначим через A наименьшее из данных 39 чисел, которое делится на 10 и в разряде десятков имеет цифру, отличную от 9. Тогда числа A + 1, A + 2, … , A + 19 также входят в рассматриваемые 39 чисел. Обозначим через S(M) сумму цифр числа M. Тогда, очевидно, S(A + 1) = S(A) + 1, S(A + 2) = S(A) + 2, … ,S(A + 9) = S(A) + 9, и S(A + 19) = S(A) + 10, Остаётся заметить, что среди 11 последовательных чисел A, A + 1, … , A + 10 всегда есть одно, делящееся на 11.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 11 класс >> 1-й день | Убрать решения |