Задача 1:
На клетчатой бумаге нарисована прямоугольная таблица размером
2n × 2m клеток (n и m — натуральные числа).
Рассматриваются отрезки длины
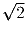
клетки каждый с
концами в узлах таблицы. Какое
наибольшее число таких отрезков,
попарно не имеющих общих точек, можно провести
в этом прямоугольнике?
Задача 2: Диагонали параллелограмма, отличного от прямоугольника,
ABCD пересекаются в точке O.
Докажите, что точка O, а также основания перпендикуляров,
опущенных из точки A на прямые BC, BD и CD, лежат на
одной окружности.
Задача 3:
Рассматривается система двух уравнений с двумя неизвестными:
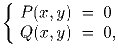
где P(x,y) и Q(x,y) —
многочлены по переменной x и по переменной y. Может ли эта
система иметь ровно три решения: (2;3), (0;2), (9;7)?
Задача 4:
Средним гармоническим чисел a и b называется число
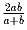
. Построить бесконечную последовательность
(или доказать, что такой не существует)
целых чисел, в которой каждый член, начиная со второго, равен
среднему гармоническому предшествующего и последующего членов
и в которой не все члены равны.


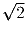 клетки каждый с
концами в узлах таблицы. Какое
наибольшее число таких отрезков,
попарно не имеющих общих точек, можно провести
в этом прямоугольнике?
клетки каждый с
концами в узлах таблицы. Какое
наибольшее число таких отрезков,
попарно не имеющих общих точек, можно провести
в этом прямоугольнике?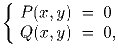 где P(x,y) и Q(x,y) —
многочлены по переменной x и по переменной y. Может ли эта
система иметь ровно три решения: (2;3), (0;2), (9;7)?
где P(x,y) и Q(x,y) —
многочлены по переменной x и по переменной y. Может ли эта
система иметь ровно три решения: (2;3), (0;2), (9;7)?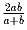 . Построить бесконечную последовательность
(или доказать, что такой не существует)
целых чисел, в которой каждый член, начиная со второго, равен
среднему гармоническому предшествующего и последующего членов
и в которой не все члены равны.
. Построить бесконечную последовательность
(или доказать, что такой не существует)
целых чисел, в которой каждый член, начиная со второго, равен
среднему гармоническому предшествующего и последующего членов
и в которой не все члены равны.