Задача 1:
Особенности национальной рыбалки.
Рыбаки из деревни Ёлкино говорят только правду, рыбаки из деревни
Палкино — только ложь, а рыбаки из деревни Стрелкино говорят
попеременно правду и ложь. Кто-то из рыбаков звонит приятелю
в город: «Только у нас на пруду отменный клёв." Приятель, не
узнав по голосу говорившего, спрашивает: «Куда ехать?" «В Стрелкино"
— отвечают ему. В какую деревню нужно ехать на рыбалку?
Задача 2:
Докажите, что если для сторон треугольника a, b и c
выполнено неравенство a + b ≥ 3c,
то c — наименьшая сторона треугольника.
Задача 3:
Докажите тождество:
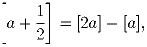
где [a] — целая часть числа a, то есть наибольшее целое
число, не превосходящее a.
Задача 4:
Пусть a, b, c и d — целые числа. Докажите, что число
A = (b – a)(c – a)(d – a)(d – c)(d – b)(c – b)
делится на 12.