 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 7 класс >> 1-й день | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Областной тур. 7 класс. 1-й день |
|
|
Решение: Звонивший не может быть из Ёлкино — иначе были бы истинны оба утверждения, а они противоречат друг другу. Не может он быть и из Стрелкино — иначе первое утверждение — истина, второе — ложь, и снова налицо противоречие. Итак, звонил рыбак из Палкино, поэтому оба утверждения неверны. Из первого утверждения следует, что клюёт не только в Палкино (при этом есть ли клёв в самом Палкино — неизвестно), а из второго — что в Стрелкино ехать не надо. Таким образом, ехать надо в Ёлкино. Задача 2: Докажите, что если для сторон треугольника a, b и c выполнено неравенство a + b ≥ 3c, то c — наименьшая сторона треугольника.
Решение: В силу неравенства треугольника a + c > b, а по условию a + b ≥ ≥ 3c. Сложив почленно эти неравенства, получаем a > c. Аналогично доказывается, что b > c. Задача 3: Докажите тождество:
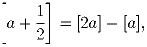
Решение: Пусть a = m + b, где m и b — соответственно целая и дробная части числа a (0 ≤ b < 1). Возможны два случая:
I. 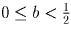 . Тогда
. Тогда 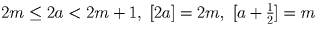 ,
и неравенство доказано.
,
и неравенство доказано.
II. 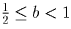 . Тогда 2m + 1 ≤ 2a < 2m + 2, [2a] = 2m + 1,
. Тогда 2m + 1 ≤ 2a < 2m + 2, [2a] = 2m + 1,
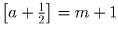 ,
и неравенство тоже доказано.
,
и неравенство тоже доказано.
Задача 4: Пусть a, b, c и d — целые числа. Докажите, что число A = (b – a)(c – a)(d – a)(d – c)(d – b)(c – b) делится на 12.
Решение: По принципу Дирихле среди чисел a, b, c и d найдутся два (без ограничения общности a и b), имеющих равные остатки при делении на 3. Тогда число b – a, а следовательно, и число A делится на 3. Остаётся доказать делимость A на 4. Если среди чисел a, b, c и d найдутся три числа одинаковой чётности, то все три разности, ими образуемые, делятся на 2, откуда A делится на даже на 8. В противном случае среди рассматриваемых чисел ровно 2 чётных (значит, разность между ними чётна) и 2 нечётных (разность между ними также чётна). Значит из 6 сомножителей, составляющих A, есть 2 чётных, и делимость A на 4 доказана.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 7 класс >> 1-й день | Убрать решения |