Задача 1:
Дан прямоугольник со сторонами 3 и 6 см, в котором расположены 8
точек. Докажите, что среди них найдутся 2 точки, расстояние между которыми
не больше

.
Задача 2:
Первой точкой Брокара в треугольнике ABC называется такая точка
P, что ∠ PAC = ∠ PCB = ∠ PBA. Пусть прямые AP, BP
и CP пересекают описанную окружность треугольника ABC в точках
A
1, B
1 и C
1. Докажите, что ∆ ABC = ∆ A
1B
1C
1.
Задача 3:
Пусть действительные числа x, y и z удовлетворяют
неравенству
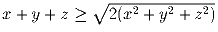
. Докажите, что тогда
|x| + |y| + |z| = x + y + z.
Задача 4:
Верно ли, что число 1999²ººº – 1 делится
a) на 1 000 000?
б) на 10 000 000?


 .
.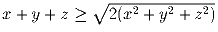 . Докажите, что тогда
|x| + |y| + |z| = x + y + z.
. Докажите, что тогда
|x| + |y| + |z| = x + y + z.