Задача 1:
Двое играют в «морской бой" по следующим правилам:
Первый игрок расставляет на полоске клетчатой бумаги
размера 1 × 100 клеток произвольное количество кораблей
(возможно, ни одного) размера
1 × 3 клетки (расстояние между любыми различными кораблями не
менее 1 клетки). Второй указывает противнику n клеток (0 ≤ n ≤ 100),
по которым он одновременно производит выстрелы, после чего про каждую из
этих клеток получает сообщение «попал" или «мимо". Второй игрок
выигрывает, если после этого он может однозначно указать количество
кораблей противника и их расположение. При каком наименьшем n второй
игрок может гарантировать себе выигрыш?
Задача 2:
Пусть O — центр вписанной окружности треугольника ABC.
На прямой BC отметим точки A
1 и A
2, на прямой AC —
точки B
1 и B
2, а на прямой AB — точки C
1 и C
2
так, что OA
1 = OA
2 = OA, OB
1 = OB
2 = OB, OC
1 = OC
2 = OC.
Докажите, что A1A2 + B1B2 + C1C2 = AB + BC + AC.
Задача 3:
Пусть действительные числа a
1, a
2, b
1, b
2, c
1, c
2
удовлетворяют неравенствам:
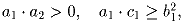
и
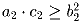
. Докажите, что (a
1 + a
2)(c
1 + c
2) ≥ (b
1 + b
2)²
Задача 4:
Докажите, что выражение 2x + 3y (x, y — целые числа)
делится на 17 тогда и только тогда, когда делится на 17 выражение
9x + 5y.


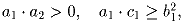 и
и
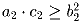 . Докажите, что (a1 + a2)(c1 + c2) ≥ (b1 + b2)²
. Докажите, что (a1 + a2)(c1 + c2) ≥ (b1 + b2)²