 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 9 класс >> 2-й день | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Областной тур. 9 класс. 2-й день |
|
|
Решение:
ОТВЕТ: n = 50. Занумеруем поля числами от 1 до 100 по порядку. Если указать менее 50 полей, то найдётся 4 идущих подряд поля, среди которых указано не более одного. Без ограничения общности это поля 1, 2, 3 и 4. Теперь если указано поле 1 (аналогично, поле 4), то при ответе «промах" на все указанные поля невозможно определить, стоит корабль на полях 2, 3, 4 или нет. Если же указанное поле 2 или 3, то при ответе «попал" на это поле и «промах" на все остальные поля, нельзя определить как расположен единственный корабль противника: 1 – 2 – 3, или 2 – 3 – 4.
50 полей достаточно. В самом деле, укажем все поля с нечётными номерами. Тогда при любом ответе расположение флота противника определяется однозначно: если на пару полей n и n + 2 получен ответ «попал", то на полях n, n + 1, n + 2 стоит корабль. Если при попадании на поле номер n имеются промахи на полях n – 2 и n + 2, то корабль стоит полях n – 1, n, n + 1.
Задача 2: Пусть O — центр вписанной окружности треугольника ABC. На прямой BC отметим точки A1 и A2, на прямой AC — точки B1 и B2, а на прямой AB — точки C1 и C2 так, что OA1 = OA2 = OA, OB1 = OB2 = OB, OC1 = OC2 = OC.Докажите, что A1A2 + B1B2 + C1C2 = AB + BC + AC.
Решение: Пусть P ∈ [AC], K ∈ [AB] и T ∈ [AC] — точки касания вписанной окружности со сторонами треугольника (см. рис.21). Тогда ∆ AOT = ∆ A1OP (они прямоугольные, имеют равные катеты OP = OT, и гипотенузы OA = OA1, поэтому AT = A1P. Аналогично, AK = A2P, KB = BP = B1T = B2T, PC = TC = C1K = C2K. Имеем: A1A2 + B1B2 + C1C2 = A1P + PA2 + B1T + + TB2 + C1K + KC2 = AT + AK + BK + BP + + PC + CT = (AT + CT) + (AK + KB) + + (BP + PC) = AC + AB + BC, что и требовалось доказать.
Задача 3: Пусть действительные числа a1, a2, b1, b2, c1, c2 удовлетворяют неравенствам:
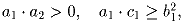 и
и
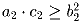 . Докажите, что (a1 + a2)(c1 + c2) ≥ (b1 + b2)²
. Докажите, что (a1 + a2)(c1 + c2) ≥ (b1 + b2)²Решение: Рассмотрим квадратные трёхчлены y1 = a1x² + 2b1x + c1 и y2 = a2x² + 2b2x + c2. Согласно условию их дискриминанты неположительны, поэтому график каждого из них не пересекает ось абсцисс. Кроме того, их старшие коэффициенты имеют один и тот же знак, поэтому оба графика лежат в одной и той же полуплоскости относительно OX. Так как трёхчлен y = (a1 + a2)x² + 2(b1 + b2)x + (c1 + c2) есть сумма многочленов y1 и y2, его график также не пересекает ось абсцисс, т.е. его дискриминант неположителен, что и надо доказать.
Задача 4: Докажите, что выражение 2x + 3y (x, y — целые числа) делится на 17 тогда и только тогда, когда делится на 17 выражение 9x + 5y.
Решение: Заметим, что 5(2x + 3y) – 3(9x + 5y) = – 17x делится на 17, поэтому из деления на 17 числа 2x + 3y следует деление на 17 чисел 5(2x + 3y), 5(2x + 3y) + 17x = 3(9x + 5y) и наконец, 9x + 5y и наоборот.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Областной тур >> 9 класс >> 2-й день | Убрать решения |