Задача 1:
Пусть a, b и c — целые неотрицательные числа такие, что
28a + 30b + 31c = 365.
Найдите все значения, которые может принимать сумма a + b + c.
Задача 2:
В каждую клетку таблицы (2n + 1) × (2n + 1) записано
число +1 или -1. Пусть
p
i — произведение чисел i-ой строки, q
j — произведение чисел
j-го столбца. Докажите, что
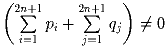
.
Задача 3:
Из квадрата 5 × 5 вырезали центральную клетку. Как разрезать
получившуюся плоскую фигуру на 2 части, которыми целиком можно обклеить
куб 2 × 2 × 2?
Задача 4:
Числа x, y и z удовлетворяют равенству
x + y + z – 2(xy + yz + zx) = ½ – 4xyz. Докажите, что хотя бы одно
из них равно ½.


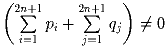 .
Задача 3:
Из квадрата 5 × 5 вырезали центральную клетку. Как разрезать
получившуюся плоскую фигуру на 2 части, которыми целиком можно обклеить
куб 2 × 2 × 2?
.
Задача 3:
Из квадрата 5 × 5 вырезали центральную клетку. Как разрезать
получившуюся плоскую фигуру на 2 части, которыми целиком можно обклеить
куб 2 × 2 × 2?