Задача 1:
Решите систему уравнений относительно x и y:
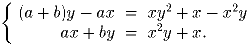
(a и b — заданные отрицательные числа).
Задача 2:
Дедушка, бабушка, папа и мама подошли ночью к мосту (с одной стороны)
и хотят перейти через него. У них есть на всех один фонарик, без которого
невозможно и шага ступить. Мост выдерживает только двух человек. Папа
может перейти мост за 1 минуту, мама — за 2 минуты, дедушка — за
5 минут, бабушка — за 10 минут. Как им всем перейти мост за 17
минут?
Задача 3:
Выпуклый пятиугольник вписан в окружность. Известно, что все его
диагонали равны между собой. Докажите, что все его внутренние углы
равны между собой, и что все его стороны также равны между собой.
Задача 4:
Является ли число 4
9 + 6¹º + 3²º простым?