 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 10 класс | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Заочный тур. 10 класс |
|
|
Решение: Первый способ: Рассмотрим функцию
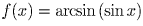 — её график изображён на рис.11. Видно,
что график требуемой функции (он изображён на рис.12) получается из
графика f(x) путём сдвигов и сжатий. Теперь легко получаем, что
требуемая функция имеет вид:
— её график изображён на рис.11. Видно,
что график требуемой функции (он изображён на рис.12) получается из
графика f(x) путём сдвигов и сжатий. Теперь легко получаем, что
требуемая функция имеет вид: 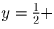
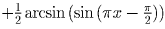 .
.Второй способ: Рассмотрим функцию f(x) = x (дробная часть x) — её график — на рис.13. Очевидно, наша функция совпадает с функцией f на промежутках [2n;\,2n + 1], где n — целое число. На промежутках [2n – 1;\,2n] (n — целое) y совпадает с функцией 2 – x. Это приводит к формуле: y = ( – 1)[x]x + 1 – ( – 1)[x] (здесь [x] — целая часть числа x).
Задача 2: В круге отметили точку A, а на границе этого круга — точки B и C. С помощью циркуля и линейки постройте прямую, делящую на две равновеликие части выпуклую фигуру, ограниченную отрезками AB и AC и дугой BC.
Решение: Построим такую прямую, проходящую через точку M — середину дуги BC.
Исследование. Пусть задача решена, и такая прямая l построена. Очевидно, l не может пересекать дуги MB и MC, поэтому она пересекает ломаную BAC; обозначим точку пересечения буквой L. Пусть T — середина хорды BC (см.рис.14). Тогда отрезок MT делит сегмент BMC на равные части; отрезок AT, будучи медианой треугольника ∆ ABC, делит его на два равновеликих треугольника, поэтому ломаная MTA делит расматриваемую фигуру на 2 части равной площади. Но тогда отрезок AT пересекает отрезок ML в некоторой точке (назовём её O), причём площади треугольников ∆ LOA и ∆ TOM равны. Значит, равны площади треугольников ∆ AMT и ∆ AML, откуда точки L и T равноудалены от прямой AM, т.е. четырёхугольник MTLA — трапеция.
Построение. Проведём через середину хорды BC (точку T) прямую, параллельную прямой MA, и обозначим через L точку её пересечения с ломаной BAC. Тогда прямая ML искомая.
Доказательство.
Без ограничения общности полагаем, что L ∈ AB. Пусть O —
точка пересечения диагоналей трапеции MALT. По свойству трапеции
S ∆ MOT = S ∆ LOA, откуда
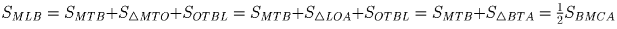 .
.
Анализ. Поскольку фигура выпуклая, через каждую точку её границы (значит, и через точку M) проходит единственная прямая, делящая пополам её площадь.
Задача 3: Голодный ёжик нашёл сейф с едой. Сейф оказался заперт на кодовый замок, который состоит из 100 кнопок с лампочками, расположенными в квадрате 10 × 10. При нажатии на любую кнопку все лампочки, стоящие с ней в одном ряду (как горизонтальном, так и вертикальном) общим числом 19 штук меняют своё состояние (загораются или гаснут). Лишь когда все кнопки зажгутся, ёжик дорвётся до желанной еды. Сколько кнопок должен нажать ёжик, чтобы как можно скорее открыть сейф?
Решение:
Первый способ: Пусть некоторая кнопка A не была нажата. Покажем, что тогда сейф не может быть открыт. Действительно, рассмотрим 19 лампочек, стоящих с A в одном ряду (горизонтальном или вертикальном). Изначально ни одна из них не зажжена. При каждом нажатии кнопки, не стоящей с A в одном ряду меняют своё состояние ровно 2 из рассматриваемых лампочек, при любом другом нажатии — ровно 10 (A не нажималась!), т.е. всегда чётное число. Значит, среди этих 19 лампочек зажжено только чётное число, и сейф заперт.
Очевидно, что если все кнопки были нажаты по разу, то каждая лампочка поменяла своё состояние 19 раз, поэтому она зажжена
Второй способ: Если ёжик нажмёт все кнопки по разу, то каждая лампочка изменит своё состояние 19 раз, т.е. загорится. Покажем, что меньшим числом нажатий не обойтись. Пусть, от противного, нам удалось открыть сейф, нажав не все кнопки. Можно полагать, что никакая кнопка не нажималась более одного раза (двойное нажатие кнопки эквивалентно тому, что данная кнопка вообще не нажималась). Рассмотрим произвольную лампочку. Чтобы она зажглась, необходимо, чтобы из 19 кнопок, стоящих с ней в одном ряду (горизонтальном или вертикальном), было нажато нечётное число, поэтому найдётся ряд I (без ограничения общности вертикальный) в котором нажато нечётное число кнопок. Рассмотрим произвольный горизонтальный ряд. Если кнопка, стоящая на пересечении этого ряда с рядом I не нажималась, то во всём горизонтальном ряду нажато чётное число кнопок (такой ряд назовём чётным), а если нажималась — то нечётное число (ряд нечётный). Получается, что всего нечётных рядов нечётное количество, а потому всего нажато нечётное число кнопок. С другой стороны при каждом нажатии меняет своё состояние нечётное число лампочек, и так как в результате поменяли состояние все 100 лампочек, было осуществлено чётное число нажатий. Противоречие.
Ответ: все 100 кнопок.
Задача 4: Докажите, что для всякого простого числа p, большего трёх, число p² – 1 делится на 24.Решение: p² – 1 = (p – 1)(p + 1). Так как p — простое, и p > 3, числа p – 1 и p + 1 — последовательные чётные числа, значит одно из них делится на 4, другое — на 2. Таким образом, p² – 1 делится на 8. Числа p – 1, p, p + 1 — последовательные в натуральном ряду, значит из них одно делится на 3, и это не p. Значит, p² – 1 делится ещё и на 3, что завершает доказательство.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 10 класс | Убрать решения |