Задача 1:
Найдите все пары чисел x и y, которые удовлетворяют уравнению:
tg 4x + tg 4y + 2 ctg ²x ctg ²y = 3 + sin ²(x + y).
Задача 2:
Докажите, что любую замкнутую ломаную на плоскости, длина которой
равна 1, можно покрыть кругом радиуса
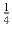
.
Задача 3:
Красящий хамелеон — сказочная шахматная фигура, которая с любого
поля доски ходит на соседнее поле по горизонтали или вертикали. При
этом она либо красит вновь занимаемое поле в свой цвет, либо сама
окрашивается в цвет поля, на которое она перешла. На шахматную доску
8 × 8, все поля которой синие, поставили зелёного хамелеона.
Указать все раскраски доски в синий и зелёный цвета (каждое поле в
свой цвет), которые можно получить за несколько ходов.
Задача 4:
Можно ли составить магический квадрат из чисел 1, 2, … , 25
(каждое число встречается ровно один раз) так, чтобы сумма восьми чисел,
стоящих в заштрихованных клетках (см. рисунок), делилась бы на 3?
(Квадрат называется магическим, если суммы чисел в каждой строке, в каждом
столбце и в каждой из двух больших диагоналей равны между собой.)


 .
.