 |
 |
|
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 11 класс | Убрать решения |
|
|
| XXXIX Екатеринбургская городская олимпиада, 1998-1999. Заочный тур. 11 класс |
|
|
tg 4x + tg 4y + 2 ctg ²x ctg ²y = 3 + sin ²(x + y).
Решение: Преобразуем левую часть уравнения:
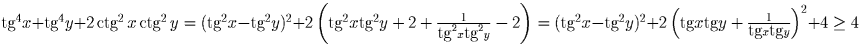 ,
причём равенство имеет место тогда и только тогда, когда
tg ²x – tg ²y = 0, и tg x tg y = 1.
,
причём равенство имеет место тогда и только тогда, когда
tg ²x – tg ²y = 0, и tg x tg y = 1.Так как правая часть не больше 4, уравнение имеет решение только если обе его части равны 4. Имеем систему:
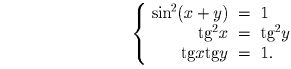
Из первого уравнения находим 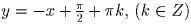 , а
из второго и третьего — tg x = tg y или (после подстановки в него
y) tg x = ctg x, откуда
, а
из второго и третьего — tg x = tg y или (после подстановки в него
y) tg x = ctg x, откуда 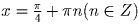 . Тогда
. Тогда
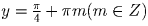 . Проверкой убеждаемся, что полученные
значения переменных действительно решают систему.
. Проверкой убеждаемся, что полученные
значения переменных действительно решают систему.
Ответ: 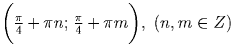 .
.
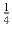 .
.Решение: Рассмотрим произвольную точку ломаной A, и отметим на ломаной точку B так, что точки A и B делят ломаную на две равные по длине части. Пусть M — середина отрезка AB. Докажем, что круг с центром в точке M радиуса
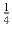 покрывает всю ломаную, то
есть, что расстояние от произвольной точки ломаной до M не больше
покрывает всю ломаную, то
есть, что расстояние от произвольной точки ломаной до M не больше
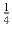 . Пусть C — произвольная точка ломаной. Тогда сумма
длин отрезков AC и BC не превосходит половины длины ломаной, то
есть не превосходит
. Пусть C — произвольная точка ломаной. Тогда сумма
длин отрезков AC и BC не превосходит половины длины ломаной, то
есть не превосходит 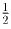 . Теперь если точка C не лежит на
прямой AB, то CM — суть медиана треугольника ABC, и по
известной теореме её длина меньше полусуммы сторон, её заключающих,
то есть меньше
. Теперь если точка C не лежит на
прямой AB, то CM — суть медиана треугольника ABC, и по
известной теореме её длина меньше полусуммы сторон, её заключающих,
то есть меньше 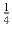 . Если же C лежит на прямой AB, то,
очевидно, CM в точности равно
. Если же C лежит на прямой AB, то,
очевидно, CM в точности равно 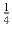 . Утверждение доказано.
Задача 3:
Красящий хамелеон — сказочная шахматная фигура, которая с любого
поля доски ходит на соседнее поле по горизонтали или вертикали. При
этом она либо красит вновь занимаемое поле в свой цвет, либо сама
окрашивается в цвет поля, на которое она перешла. На шахматную доску
8 × 8, все поля которой синие, поставили зелёного хамелеона.
Указать все раскраски доски в синий и зелёный цвета (каждое поле в
свой цвет), которые можно получить за несколько ходов.
. Утверждение доказано.
Задача 3:
Красящий хамелеон — сказочная шахматная фигура, которая с любого
поля доски ходит на соседнее поле по горизонтали или вертикали. При
этом она либо красит вновь занимаемое поле в свой цвет, либо сама
окрашивается в цвет поля, на которое она перешла. На шахматную доску
8 × 8, все поля которой синие, поставили зелёного хамелеона.
Указать все раскраски доски в синий и зелёный цвета (каждое поле в
свой цвет), которые можно получить за несколько ходов.Решение:
Ответ: Все раскраски кроме «шахматной".
Докажем, что «шахматную" раскраску получить нельзя. Предположим противное и рассмотрим последнее поле, которое было перекрашено. Пусть, например, оно стало в результате зелёным. Тогда все соседние по горизонтали и вертикали поля к этому моменту уже получили итоговую окраску, то есть все они синие. Но с синего поля может прийти хамелеон только синего цвета, а тогда он не сможет перекрасить рассматриваемое поле. Противоречие.
Зафиксируем теперь произвольную окраску доски, отличную от "шахматной" и приведём один из возможных алгоритмов, позволяющих её получить. Выберем пару соседних полей, которые должны быть одного цвета (например, синего) — ясно, что такая найдётся. Рассмотрим какой-нибудь квадрат 2 × 2, содержащий выбранную пару (назовём его особым), и, поставив изначально хамелеона на одно из двух других полей этого квадрата, перекрасим два других поля в зелёный цвет. Занумеруем поля доски натуральными числами от 1 до 64, соблюдая следующие правила: 1) поля особого квадрата нумеруются числами 1 — 4, причём выбранная пара синих полей имеют номера 1 и 2. 2) До любого поля с номером n,\,n ≥ 4 можно добраться хамелеоном как с одного из полей 3 и 4, проходя только по клеткам с номерами от 5 до (n – 1), так и с одного из полей 1 и 2, проходя только по клеткам с номерами от 5 до (n – 1) и, возможно, по одной из клеток с номером 3 и 4. (Занумеровать поля таким образом несложно). Теперь раскрашиваем поля доски в порядке убывания их номеров. Для покраски поля номер n,n ≥ 5 становимся хамелеоном на поле особого квадрата того же цвета, что и n-ое поле, и движемся к нему хамелеоном по полям с номерами от 5 до n, (по пути перекрашивая все эти поля в цвет хамелеона), закрашиваем клетку номер n, движемся обратно тем же путём и если нам пришлось перекрасить клетку 3 или 4 — восстанавливаем её цвет, перемещая хамелеона внутри особого квадрата. Ясно, что при этом окраска полей с номерами, большими n (равно как и полей особого квадрата) не меняется. Перекрасить одно или оба из полей 3 и 4 в синий цвет (если это необходимо), не меняя цвета остальных — тривиальная задача, а поля 1 и 2 уже покрашены так, как надо. Требуемая раскраска доски получена.
Задача 4: Можно ли составить магический квадрат из чисел 1, 2, … , 25 (каждое число встречается ровно один раз) так, чтобы сумма восьми чисел, стоящих в заштрихованных клетках (см. рисунок), делилась бы на 3? (Квадрат называется магическим, если суммы чисел в каждой строке, в каждом столбце и в каждой из двух больших диагоналей равны между собой.) Решение:Предположим, что такой магический квадрат существует. Обозначим
сумму чисел, стоящих в каждой из строк (столбцов, диагоналей)
S. Сумму чисел, стоящих в отмеченных клетках получим, если из
суммы всех чисел от 1 до 25 (а это ровно 5S)
отнимем числа стоящие на диагоналях,
в средней строке и в среднем столбце. Каждая такая сумма равна
S, но при этом центральная клетка учтена четырежды, значит
(если в ней стоит число a) искомая сумма
равна 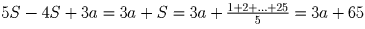 — на 3 не делится. Противоречие.
— на 3 не делится. Противоречие.
Замечание: В действительности мы доказали большее, а именно, что во всяком магическом квадрате из чисел от 1 до 25, сумма чисел в указанных клетках может принимать только одно из значений: 68,\,71,\,74,\, … ,140.
| Задачная база >> Другие города России >> Екатеринбургские соревнования >> Областная олимпиада >> XXXIX олимпиада, 1998-1999 >> Заочный тур >> 11 класс | Убрать решения |