Задача 1:
Докажите, что для всякого положительного числа a хотя бы одно из чисел

и
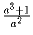
не меньше двух.
Задача 2:
Назовём диагональ многоугольника хорошей, если она делит его
на две фигуры равной площади. Какое наибольшее число хороших
диагоналей может иметь выпуклый пятиугольник?
Задача 3:
Пончик закусывал в придорожном кафе, когда мимо него прошёл
автобус. Через 3 плюшки мимо Пончика проехал мотоцикл, а ещё через
3 — автомобиль. Мимо Сиропчика, который закусывал в другом кафе
у того же шоссе, они проехали в таком порядке: автобус, через 3
плюшки — автомобиль и ещё через 3 — мотоцикл. Скорость автомобиля
равна 60 км/ч, мотоцикла — 30 км/ч. Чему равна скорость автобуса, если
Пончик и Сиропчик поглощают плюшки с одной и той же одинаковой скоростью?
Задача 4:
Можно ли так вписать в таблицу 8 × 8 числа от 1 до 64
(каждое число ровно
1 раз), так чтобы сумма любых двух чисел, стоящих в клетках, имеющих
общую сторону или вершину, не делилась бы на 4?


 и
и 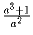 не меньше двух.
Задача 2:
Назовём диагональ многоугольника хорошей, если она делит его
на две фигуры равной площади. Какое наибольшее число хороших
диагоналей может иметь выпуклый пятиугольник?
не меньше двух.
Задача 2:
Назовём диагональ многоугольника хорошей, если она делит его
на две фигуры равной площади. Какое наибольшее число хороших
диагоналей может иметь выпуклый пятиугольник?