Задача 1: Докажите, что если числа a, b, c и d таковы, что 0 ≤ a ≤ 1,\ 0 ≤ b ≤ 1, 0 ≤ c ≤ 1, 0 ≤ d ≤ 1, то справедливо неравенство: (a + b + c + d + 1)² ≥ 4(a² + b² + c² + d²).

Задача 2: На продолжении стороны AC треугольника ABC за точку A отмечена точка D. С помощью циркуля и линейки постройте на стороне BC точку E такую, что площади треугольников DEC и ABC равны.

Задача 3: В треугольнике площади 2 расположены 15 точек, никакие три из которых не лежат на одной прямой. Докажите, что существует треугольник с вершинами в этих точках, площадь которого меньше, чем .

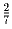
Задача 4: Назовём трёхзначное число особенным, если из него можно вычеркнуть цифру так, что образовавшееся число будет меньше суммы цифр исходного трёхзначного. Сколько существует особенных чисел?
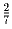