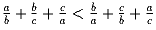Задача 1: Докажите, что для любых действительных чисел a,b и c таких, что a > b > c > 0, выполнено неравенство

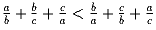
Задача 2: На координатной плоскости построены две параболы: y = x² + 4, y =  – x² + 2x, и к ним проведены две общие касательные. Докажите, что четырехугольник с вершинами в точках касания является параллелограммом.

Задача 3: На шахматную доску размера (2n – 1) × (2n – 1) поставили 2n – 1 ладью так, что ни одна из них не бьет другую. Докажите, что в любом квадрате n × n стоит хот бы одна ладья.

Задача 4: Точки E и F – середины сторон AB и AD параллелограмма ABCD, а отрезки CE и BF пересекаются в точке K. Точка M лежит на отрезке EC, причем BM || KD. Докажите, что площади треугольника KFD и трапеции KBMD равны.

Задача 5: Для каких натуральных чисел n числа 1,2,3,…,4n можно разбить на n групп по 4 числа так, чтобы в каждой группе одно из чисел равнялось среднему арифметическому трех остальных?