 |
 |
|
| Задачная база >> Другие города России >> Пермские соревнования >> Областной турнир Юных математиков >> I >> Турнир матбоёв >> 6 - 7 класс >> Матбой 3. III-V лиги | Убрать решения |
|
|
| I Пермский областной турнир Юных математиков. Турнир матбоёв. 6 - 7 класс. Матбой 3. III-V лиги |
|
|
Решение: Сыну завещано в 2 раза больше, чем матери, а жене – в 2 раза больше, чем дочери. Значит, наследство нужно разделить в отношении 4:2:1. Задача 2: Сумма двух чисел больше их произведения, но меньше их разности. Выяснить, положительны или отрицательны эти числа.
Решение: ab < a + b < a – b. Так как a + b < a – b, то b < 0. Так как ab < a + b, а b < 0, то a > 0 (иначе ab > 0, a + b < 0, то есть ab > a + b). Итак, b < 0, a > 0. Задача 3: Имеется 37 карточек, каждая из которых выкрашена с одной стороны в зелёный, а с другой стороны - в синий цвет. Карточки разложены подряд в виде полосы так, что у 9 карточек сверху оказался синий цвет. За один ход разрешается перевернуть любые 20 карточек. Можно ли за несколько ходов добиться того, чтобы полоса стала полностью зелёной? А полностью синей? Если можно, то какое наименьшее число ходов для этого потребуется?
Решение: Предположим, что первым ходом мы x «синих" карточек сделали «зелёными". После этого полоса будет содержать (9 – x) + (20 – x) = 29 – 2x «синих" карточек и x + (28 – (20 – x)) = 2x + 8 «зелёных". Таким образом, перед вторым ходом, как и перед первым,«синих" карточек будет нечётное число, а«зелёных" - чётное. Очевидно, эта закономерность сохранится для любого числа ходов, то есть мы никогда не получим того, чтобы число«синих" карточек стало равным нулю (чётным числом). Это значит, что сделать всю полосу зелёной нельзя. Так как после первого хода число«зелёных" карточек осталось чётным (2x + 8), то можно взять x таким, чтобы 2x + 8 = 20, то есть при x = 6. Итак, если первым ходом 6 «синих" карточек сделать«зелёными" и 14 «зелёных" – «синими", то уже вторым ходом можно всю полосу сделать синей.
Задача 4: Король Артур заказал художнику рисунок для своего щита, имеющего форму четверти круга, с просьбой окрасить его в три цвета: жёлтый - цвет доброты, красный – храбрости, синий – мудрости. Когда художник принёс рисунок, оруженосец короля сказал, что на рисунке храбрости больше, чем мудрости, и это не понравилось королю – ведь это король! Однако художник смог доказать, что на рисунке и того, и другого поровну. Как? Дополнительно узнайте, чего больше у короля: доброты или мудрости и храбрости вместе взятых? (Можно использовать тот факт, что если радиус одного круга в 2 раза больше радиуса другого круга, то площадь первого в 4 раза больше площади второго круга.)
Решение: Две половинки маленьких кружочков в сумме составляют четверть большого круга, так как радиус маленького круга в 2 раза меньше радиуса большого круга. Введём обозначения а, х, y и составим уравнение 2a + x + y = 2a + 2x, откуда х = y. Доброты у короля больше. Задача 5: Разделите циферблат на 4 части так, чтобы сумма чисел в каждой из них составляла 15. Число, состоящее из 2 цифр может быть разделено на 2 числа, например, 11 можно считать и как 1 + 1 = 2.
Решение: Можно, например, так: 8 + 7,6 + 9,10 + 1(11) + 1(12) + 1 + 2,1(11) + 2(12) + 3 + 4 + 5. Задача 6: Станции наблюдения с номерами от 183 до 282 расположены по кругу и соединены между собой так, что каждая из них может передать сведения непосредственно только на станцию, находящуюся от неё седьмой по счёту (по часовой стрелке). Может ли начальник станции 225 поздравить с днём рождения своего друга на станции 200 (естественно, с помощью промежуточных станций)?
Решение: Может. 225 + 7 • 8 = 281, 281 → 188, 188 + 7 • 13 = 279, 279 → 186, 186 + 7 • 2 = 200. Задача 7: Существует ли трёхзначное число, равное произведению своих цифр?
Решение: Пусть
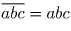 , то есть 100a + 10b + c = abc, но bc < 100, то есть abc < 100a, то есть 100a + 10b + c < 100a и 10b + c < 0, что недопустимо.
Задача 8:
Данный квадрат разделить ломаной на две части одинаковой площади
таким образом, чтобы каждое звено ломаной было параллельно стороне
или диагонали квадрата, причём сумма длин звеньев, параллельных
сторонам, равнялась бы длине стороны, а сумма длин звеньев,
параллельных диагоналям, равнялась бы длине диагонали. Какое
наименьшее число звеньев может иметь такая ломаная?
, то есть 100a + 10b + c = abc, но bc < 100, то есть abc < 100a, то есть 100a + 10b + c < 100a и 10b + c < 0, что недопустимо.
Задача 8:
Данный квадрат разделить ломаной на две части одинаковой площади
таким образом, чтобы каждое звено ломаной было параллельно стороне
или диагонали квадрата, причём сумма длин звеньев, параллельных
сторонам, равнялась бы длине стороны, а сумма длин звеньев,
параллельных диагоналям, равнялась бы длине диагонали. Какое
наименьшее число звеньев может иметь такая ломаная?Решение: Очевидно, что каждое звено ломаной должно быть короче параллельной ему стороны или диагонали (в противном случае уже одно такое звено разрезало бы квадрат на две части). Так как ломаная должна содержать переходы от участков, параллельных стороне квадрата, на участки, параллельные диагонали, то должно быть не менее 2-х участков каждого вида. Отсюда следует, что число звеньев ломаной не может быть меньше четырёх. Покажем теперь, что существует ломаная из четырёх звеньев, удовлетворяющая всем требованиям условия задачи. Разделим данный квадрат на 36 равных квадратов. Легко проверить, что изображенная на рисунке ломаная будет искомой.
| Задачная база >> Другие города России >> Пермские соревнования >> Областной турнир Юных математиков >> I >> Турнир матбоёв >> 6 - 7 класс >> Матбой 3. III-V лиги | Убрать решения |