 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 10 класс | Убрать решения |
|
|
| XXV всероссийская математическая олимпиада школьников. Заключительный этап. 10 класс |
|
|
На столе стоят три пустых банки из-под меда. Винни-Пух, Кролик и Пятачок по очереди кладут по одному ореху в одну из банок. Их порядковые номера до начала игры определяются жребием. При этом Винни может добавлять орех только в первую или вторую банку, Кролик – только во вторую или третью, а Пятачок – в первую или третью. Тот, после чьего хода в какой-нибудь банке оказалось ровно 1999 орехов, проигрывает. Докажите, что Винни-Пух и Пятачок могут, договорившись, играть так, чтобы Кролик проиграл.
Решение:
Пусть Винни и Пятачок вначале кладут свои орехи во вторую и третью банки, несмотря на ходы Кролика, до тех пор, пока в одной из банок не станет 1998 орехов. После этого тот, кто должен класть орехи в эту банку (пусть, например, это Винни) начинает класть их в I. При этом он уже положил во II банку не менее 999 орехов, значит, в III орехов тоже не менее 999 (туда их клал Пятачок). После этого Пятачок продолжает класть в III банку орехи, пока там не станет 1998 – это произойдёт не более, чем через 500 ходов, так как в III банку также приходится класть орехи Кролику, чтобы не проиграть. После этого Пятачок также может класть орехи в I банку, так как там не более 500 орехов, положенных Винни, а Кролик вынужден будет положить орех во II или III, где их уже по 1998.
Задача 2:
Найдите все бесконечные ограниченные
последовательности натуральных чисел a1, a2, a3, …,
для всех членов которых, начиная с третьего, выполнено
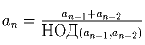 .
.
Ответ: a1 = a2 = … = 2. Пусть для каких-то двух членов последовательности ak и ak + 1 их НОД равен 1. Тогда НОД (ak,ak + 1) = НОД (ak + ak + 1,ak + 1) = НОД (ak + 2,ak + 1), т.е. для всех последующих членов последовательности НОД тоже будет равен 1. При этом, начиная с k-го члена, последовательность превращается в последовательность an = an – 1 + an – 2, которая неограниченно возрастает.
Итак, НОД всегда должен быть не меньше 2. Если какие-то члены последовательности ak и ak + 1 не равны друг другу, то ak + 2 < max (ak,ak + 1) и ak + 1 ≠ ak + 2.
Аналогично, ak + 3 < max (ak + 1,ak + 2) < max (ak,ak + 1).
Мы получили, что максимальное число в парах идущих подряд членов последовательности монотонно убывает, т. е. когда-то станет равным 1, и тогда НОД у каких-то членов тоже станет равен 1, что не должно случиться.
Итак, все члены последовательности должны равняться друг другу и их НОД = 2, т.е. an = 2.
Задача 3:Пусть окружность, вписанная в треугольник ABC, касается его сторон AB, BC и AC в точках K, L и M соответственно. К окружностям, вписанным в треугольники BKL, CLM и AKM, проведены попарно общие внешние касательные, отличные от сторон треугольника ABC. Докажите, что эти касательные пересекаются в одной точке.
Решение:
Пусть K, L, M – точки касания вписанной окружности, со сторонами AB, BC, AC соответственно, O1, O2, O3 – центры малых окружностей, так как ∠ KO1M = 90 + ( ∠ A/2), а ∠ KLM = 90° – ( ∠ A/2), то ∠ KO1M + ∠ KLM = 180, и O1 лежит на вписанной в треугольник ABC окружности. Аналогично O2 и O3 лежат на этой окружности и являются серединами дуг KL и LM. Используя результат задачи 9.3 заключаем, что построенные касательные проходят через центр окружности, вписанной в треугольник KLM, что и требовалось доказать.
Задача 4:
В квадрате n × n клеток бесконечной шахматной доски расположены n² фишек, по одной фишке в каждой клетке. Ходом называется перепрыгивание любой фишкой через соседнюю по стороне фишку, непосредственно за которой следует свободная клетка. При этом фишка, через которую перепрыгнули, с доски снимается. Докажите, что позиция, в которой дальнейшие ходы невозможны, возникнет не ранее, чем через [n²/3] ходов.
Решение:
Будем различать два типа ходов – внутренние и внешние, в зависимости от того, куда ставится фишка, делающая ход: внутрь исходного квадрата n*n клеток, или вне его.
Пусть получена позиция, где дальнейшие ходы невозможны, причём сделано k внутренних ходов и l внешних.
Ясно, что никакие две фишки не находятся в соседних клетках, а в исходном квадрате n × n не менее, чем [n²/2] клеток пусты. Так как каждый внутренний ход увеличивал количество пустых клеток не более, чем на 1, а каждый внешний – не более, чем на 2, то имеем неравенство
k + 2l ≥ [n²/2].
Предположив теперь, что n чётно, разобьём исходный квадрат на
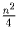 четырёхклеточных квадратиков и заметим, что на каждый квадратик пришлось не
менее двух ходов, в которых участвовали (делали ход или снимались с доски)
фишки, стоявшие в клетках этого квадратика. Поскольку в каждом внутреннем
ходе участвовали фишки не более, чем двух квадратиков, а в каждом внешнем –
не более, чем одного, то
четырёхклеточных квадратиков и заметим, что на каждый квадратик пришлось не
менее двух ходов, в которых участвовали (делали ход или снимались с доски)
фишки, стоявшие в клетках этого квадратика. Поскольку в каждом внутреннем
ходе участвовали фишки не более, чем двух квадратиков, а в каждом внешнем –
не более, чем одного, то

Из доказанных неравенств получаем 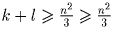 , т.е. утверждение задачи в этом случае верно.
, т.е. утверждение задачи в этом случае верно.
Легко видеть, что оно верно также при n = 1 и при n = 3.
В случае n = 2m + 1, где m > 1, в «кресте", образованном третьей сверху горизонталью и третьей слева вертикалью, выделим 2m «доминошек", а остальную часть исходного квадрата разобьём на m² четырёхклеточных квадратиков. В каждом внутреннем ходе участвовать могли фишки, принадлежащие не более, чем двум из m² + 2m рассматриваемых фигур, а в каждом внешнем – не более, чем одной. Имеем неравенство 2k + l ≥ 2m² + 2m, поскольку фишки каждого из квадратиков участвовали не менее, чем в двух ходах, а фишки каждой "доминошки" - по крайней мере в одном.
Из первого и третьего неравенств следует, что 3k + l ≥ 4m² + 4m = n² – 1. Если здесь n² ≡ 0 (mod 3)), то, очевидно,
3(k + l) ≥ n² и 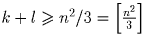 ,
в противном случае n² ≡ 1 (mod %)%3 и
,
в противном случае n² ≡ 1 (mod %)%3 и
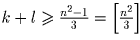 . Тем самым утверждение
задачи полностью доказано.
. Тем самым утверждение
задачи полностью доказано.
Задача 5:
Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800. Чему равна сумма цифр числа 3n?
Решение:Заметим, что 44n есть сумма 4 экземпляров числа n и 4 экземпляров числа 10n. Если складывать эти числа поразрядно, то в каждом разряде окажется сумма учетверённой цифры из этого же разряда числа n и учетверённой цифры из следующего разряда. Если при этом не происходит никаких переносов, то каждая цифра числа n складывается 8 раз, и сумма цифр во всех разрядах оказывается равной 800. При переносах же сумма цифр, очевидно, уменьшается (так как из одного разряда вычитается 10, а к другому прибавляется только 1). Поэтому в ситуации условия задачи переносов не происходит. Это означает, в частности, что любая цифра числа n не превосходит 2. Тогда при умножении n на 3 просто умножается на 3 каждая его цифра, а, значит, и сумма цифр. Поэтому сумма цифр числа 3n равна 300.
Задача 6:
В треугольнике ABC окружность, проходящая через вершины A и B, касается прямой BC, а окружность, проходящая через вершины B и C, касается прямой AB и пересекает первую окружность в точке K, K ≠ B. Пусть O – центр описанной окружности треугольника ABC. Докажите, что угол BKO – прямой.
Решение:Задача является частным случаем задачи 9.7, когда точки E и D совпадают с точкой B.
Задача 7:
Для некоторых положительных чисел x и y выполняется неравенство x² + y³ ≥ x³ + y4. Докажите, что x³ + y³ ≤ 2.
Решение: Вначале докажем, чтоx + y² ≤ x² + y³.
Допустим противное: x + y² < x² + y³, тогда, складывая это неравенство с неравенством x³ + y4 ≤ x² + y³, получим (x + x³) + (y² + y4) < 2x² + 2y³, что противоречит неравенствам x + x³ ≥ 2x² и y² + y4 ≥ y³.
Из доказанного неравенства получаем
x + y² ≥ x² + y³ ≥ x³ + y4, откуда 2x + 2y² ≥ x² + y³ + x³ + y4.
Замечая, что (1 + x²) + (1 + y4) ≥ 2x + 2y² ≥ x² + y³ + x³ + y4, получаем неравенство 2 + x² + y4 ≥ x² + y³ + x4 + y4, равносильное требуемому.
Задача 8:
В некоторой группе из 12 человек среди каждых 9 найдутся 5 попарно знакомых. Докажите, что в этой группе найдутся 6 попарно знакомых.
Решение:Возьмём граф на 12 вершинах, которые соответствуют людям, две его вершины соединены, если люди незнакомы.
Если в этом графе нет циклов нечётной длины, то его можно разбить на две части, в каждой из которых вершины не будут соединены, и поэтому найдутся 6 попарно знакомых.
Предположим теперь, что в графе есть циклы нечётной длины. Рассмотрим нечётный цикл минимальной длины. Пусть его длина равна:
а) 3. Тогда если среди 9 человек, не входящих в этот цикл, есть два незнакомых, то среди оставшихся 7 человек из каждых 4 найдутся три знакомых. Таким образом в подграфе на 7 вершинах каждые два ребра имеют общую вершину. Третье ребро обязано проходить через эту вершину. Иначе среди 4 человек не найдутся трёх знакомых. Поэтому все рёбра имеют общую вершину, и удаляя эту вершину, мы получаем 6 попарно знакомых.
б) 5. Тогда, как и выше, среди оставшихся 7 из каждых 4 найдутся 3 знакомых и среди этих 7 найдутся 6 знакомых.
в) 7. Тогда среди 5 человек, не входящих в этот цикл, все попарно знакомы. Если есть человек из цикла, знакомый со всеми этими 5, то всё доказано. В противном случае, каждый из цикла не знаком с кем-то из оставшихся. Так как 7>5, то найдётся человек A из оставшихся, не знакомый с двумя из цикла B, C . Из того, что мы взяли цикл минимальной длины, следует, что эти два незнакомых из цикла должны быть знакомы через одного D. Но тогда D знаком со всеми из пяти оставшихся, потому что удаляя из цикла D и заменяя на A, мы получаем снова цикл длины 7, а в дополнении к циклу длины 7 все попарно знакомы. г) Цикла длины 9 не может быть по условию задачи.
д) Цикл длины 11. Тогда, как и выше при рассмотрении циклов длины 7, мы видим, что оставшийся человек может быть незнаком максимум с двумя из цикла. Но тогда в цикле легко найти 5 человек, знакомых между собой и с оставшимся. (Например, взяв идущих через одного по циклу и не знакомых с оставшимся.)
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 10 класс | Убрать решения |