 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 9 класс | Показать решения |
|
|
| XXV всероссийская математическая олимпиада школьников. Заключительный этап. 9 класс |
|
|
В числе A цифры идут в возрастающем порядке (слева направо). Чему равна сумма цифр числа 9A?
Задача 2:В стране несколько городов, некоторые пары городов соединены беспосадочными рейсами одной из N авиакомпаний, причем из каждого города есть по одному рейсу каждой из авиакомпаний. Известно, что из любого города можно долететь до любого другого (возможно, с пересадками). Из-за финансового кризиса был закрыт N – 1 рейс, но ни в одной из авиакомпаний не закрыли более одного рейса. Докажите, что по-прежнему из любого города можно долететь до любого другого.
Задача 3:Треугольник ABC вписан в окружность S. Пусть A0 – середина дуги BC окружности S , не содержащей A; C0 – середина дуги AB, не содержащей C. Окружность S1 с центром A0 касается BC, окружность S2 с центром C0 касается AB. Докажите, что центр I вписанной в треугольник ABC окружности лежит на одной из общих внешних касательных к окружностям S1 и S2.
Задача 4:Числа от 1 до 1000000 покрашены в два цвета – черный и белый. За ход разрешается выбрать любое число от 1 до 1000000 и перекрасить его и все числа, не взаимно простые с ним, в противоположный цвет. Вначале все числа были черными. Можно ли за несколько ходов добиться того, что все числа станут белыми?
Задача 5:Правильный треугольник разбит на правильные треугольники со стороной 1 линиями, параллельными его сторонам и делящими каждую сторону на n частей.
Какое наибольшее число отрезков длины 1 с концами в вершинах этих треугольников можно отметить так, чтобы не нашлось треугольника, все стороны которого состоят из отмеченных отрезков?
Задача 6:Докажите, что при любом натуральном n справедливо неравенство
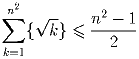
Задача 7:
Окружность, проходящая через вершины A и B треугольника ABC, пересекает сторону BC в точке D. Окружность, проходящая через вершины B и C, пересекает сторону AB в точке E и первую окружность вторично в точке F. Оказалось, что точки A, E, D, C лежат на окружности с центром O. Докажите, что угол BFO – прямой.
Задача 8:
В микросхеме 2000 контактов, первоначально любые два контакта соединены отдельным проводом. Хулиганы Вася и Петя по очереди перерезают провода, причем Вася (он начинает) за ход режет один провод, а Петя – либо один, либо три провода. Хулиган, отрезающий последний провод от какого-либо контакта, проигрывает. Кто из них выигрывает при правильной игре?
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 9 класс | Показать решения |