 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 9 класс | Убрать решения |
|
|
| XXV всероссийская математическая олимпиада школьников. Заключительный этап. 9 класс |
|
|
В числе A цифры идут в возрастающем порядке (слева направо). Чему равна сумма цифр числа 9A?
Решение:Ответ: 9. Заметим, что 9A = 10A – A. При вычитании этих чисел столбиком ни в одном разряде, кроме младшего, не приходится занимать единицу из следующего разряда. Таким образом, сумма цифр разности равна разности суммы цифр чисел 10A и A (которые равны) плюс 9.
Задача 2:
В стране несколько городов, некоторые пары городов соединены беспосадочными рейсами одной из N авиакомпаний, причем из каждого города есть по одному рейсу каждой из авиакомпаний. Известно, что из любого города можно долететь до любого другого (возможно, с пересадками). Из-за финансового кризиса был закрыт N – 1 рейс, но ни в одной из авиакомпаний не закрыли более одного рейса. Докажите, что по-прежнему из любого города можно долететь до любого другого.
Решение:Рассмотрим некоторый путь, соединяющий некоторые два города, возможно включающий в себя некоторые закрытые после кризиса рейсы. Покажем, что в этом пути любой закрытый рейс можно заменить последовательностью незакрытых. Пронумеруем авиакомпании числами от 1 до N. В одной из авиакомпаний сохранились все рейсы: предположим, что в первой. Тогда в любой другой авиакомпании закрыли по одному рейсу. Рассмотрим только рейсы первой и второй авиакомпаний: из каждого города выходит по одному рейсу этих авиакомпаний. Следовательно, все города разбиваются на циклы. В одном из этих циклов закрыли один рейс. Очевидно, можно пролететь остальными рейсами этого цикла, следовательно, мы можем «обойти» любой закрытый рейс. Отметим, что мы при этом не используем рейсы других авиакомпаний, следовательно, аналогично можно обойтись без остальных закрытых рейсов.
Задача 3:Треугольник ABC вписан в окружность S. Пусть A0 – середина дуги BC окружности S , не содержащей A; C0 – середина дуги AB, не содержащей C. Окружность S1 с центром A0 касается BC, окружность S2 с центром C0 касается AB. Докажите, что центр I вписанной в треугольник ABC окружности лежит на одной из общих внешних касательных к окружностям S1 и S2.
Решение:Из точки I проведём касательную IK к окружности S1 так, чтобы луч IK пересекал меньшую дугу A0C. Аналогичным образом проведём касательную IL к окружности S2.
Биссектриса AI угла BAC делит дугу BC на 2 равных дуги. Поэтому точки A, I, A0 лежат на одной прямой. Аналогично, на одной прямой лежат точки C, I и C0.
Из равенств
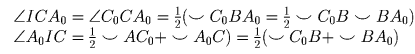
Далее, пусть D – середина отрезка BC , тогда S1 касается BC в точке D.
В прямоугольных треугольниках A0KI и A0DCкатетыA_0KиA_0DравныиA_0I=A_0Cподоказанномувыше.Следовательно,A_0KI = A_0DC.ОтсюдаA_0IK=A_0CD= A_0CB.НоA_0CB=A_0AB,(теоремаовписанномугле)иA_0AB=A_0AC.Значит,A_0IK=A_0AC,следовательнопрямаяIKпараллельнаAC.Аналогично,IL|AC,следовательноL,I,Kлежатнаоднойпрямой,параллельнойACAC.
Задача 4:
Числа от 1 до 1000000 покрашены в два цвета – черный и белый. За ход разрешается выбрать любое число от 1 до 1000000 и перекрасить его и все числа, не взаимно простые с ним, в противоположный цвет. Вначале все числа были черными. Можно ли за несколько ходов добиться того, что все числа станут белыми?
Решение:Лемма. Пусть дан набор простых чисел p1, …, pn. Тогда можно за несколько перекрашиваний добиться того, что поменяют цвет те и только те числа, которые делятся на все простые числа набора.
Доказательство. (по формуле включения-исключения): для каждого непустого поднабора чисел перекрасим числа, не взаимно простые с произведением всех чисел этого поднабора. Число, делящееся на все числа набора, перекрашивалось при каждом таком перекрашивании, всего перекрашиваний было 2n – 1, следовательно, числа, делящиеся на все числа набора перекрашены. Пусть некоторое число k не делится хотя бы на одно из чисел набора, например, на p1. Тогда оно не перекрашивалось, когда мы перекрашивали числа, не взаимно простые с p1. Остальные непустые поднаборы чисел можно разбить на пары следующим образом: поднабору, не содержащему p1, в пару ставится поднабор, полученный из него добавлением p1. При этом число k перекрашивается или при обоих перекрашиваниях пары, или ни при одном. Поэтому число k не будет перекрашено.
Лемма доказана.
Первое решение. Для каждого набора простых чисел, произведение которых не больше 1000000 , перекрасим числа, делящиеся на все эти простые числа. По лемме такая операция возможна. Докажем, что любое число k при этом будет перекрашено. Пусть k имеет m различных простых делителей, тогда оно перекрашивалось при 2l – 1 операции, то есть нечетное число раз.
Второе решение. Назовем два числа эквивалентными, если у них совпадают наборы простых делителей. Заметим, что при наших операциях классы эквивалентности перекрашиваются целиком. Будем говорить, что один класс больше другого, если если все простые делители второго класса являются делителями первого. Из леммы следует, что мы можем перекрасить любой класс, перекрасив вместе с ним только большие классы.
Сначала перекрасим минимальные классы (класс называется минимальным, если он не больше никакого другого класса). Исключим их из рассмотрения. Среди оставшихся некоторые классы станут после такого исключения минимальными. При необходимости перекрасим их и тоже исключим. И так далее.
Поскольку классов конечное число, процесс закончится.
Задача 5:
Правильный треугольник разбит на правильные треугольники со стороной 1 линиями, параллельными его сторонам и делящими каждую сторону на n частей.
Какое наибольшее число отрезков длины 1 с концами в вершинах этих треугольников можно отметить так, чтобы не нашлось треугольника, все стороны которого состоят из отмеченных отрезков?
Решение:Ответ. n(n + 1). Общее количество отрезков длины 1 равно
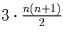 .
Все отрезки, параллельные двум сторонам большого треугольника, не
образуют треугольников, так как любой треугольник состоит из отрезков,
параллельных всем трём сторонам. Следовательно,
.
Все отрезки, параллельные двум сторонам большого треугольника, не
образуют треугольников, так как любой треугольник состоит из отрезков,
параллельных всем трём сторонам. Следовательно,
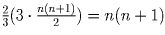 отрезков длины 1 отметить можно.
отрезков длины 1 отметить можно.
Докажем, что большее количество отрезков отметить нельзя.
Заштрихуем треугольники вида 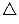 со стороной 1 (а
треугольники вида
со стороной 1 (а
треугольники вида  не будем заштриховывать).
Заштрихованные треугольники содержат все отрезки длины 1,
причём каждый отрезок принадлежит ровно одному
треугольнику. Для того, чтобы не образовался ни один из заштрихованных
треугольников, в каждом из них можно отметить не более двух отрезков.
Значит, количество выделенных отрезков не превышает ⅔
от их общего числа.
не будем заштриховывать).
Заштрихованные треугольники содержат все отрезки длины 1,
причём каждый отрезок принадлежит ровно одному
треугольнику. Для того, чтобы не образовался ни один из заштрихованных
треугольников, в каждом из них можно отметить не более двух отрезков.
Значит, количество выделенных отрезков не превышает ⅔
от их общего числа.
Задача 6:
Докажите, что при любом натуральном n справедливо неравенство
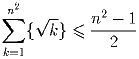
Решение:
При n = 1 неравенство обращается в равенство 0 = 0. При n > 1 докажем, что сумма дробных частей на каждом промежутке между двумя последовательными квадратами удовлетворяет неравенству
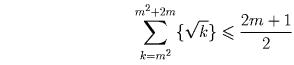
Нетрудно проверить (например, возведением в квадрат), что
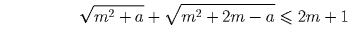
Следовательно,
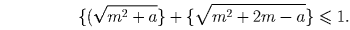
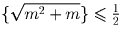 (получаемое делением на 2 обеих частей последнего
неравенства при a = m),
приходим к неравенству, записанному в начале решения. Суммируя теперь
это неравенство по всем n от 1 до n – 1 получаем
(получаемое делением на 2 обеих частей последнего
неравенства при a = m),
приходим к неравенству, записанному в начале решения. Суммируя теперь
это неравенство по всем n от 1 до n – 1 получаем
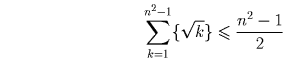
Остаётся заметить, что 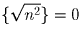 .
.
Окружность, проходящая через вершины A и B треугольника ABC, пересекает сторону BC в точке D. Окружность, проходящая через вершины B и C, пересекает сторону AB в точке E и первую окружность вторично в точке F. Оказалось, что точки A, E, D, C лежат на окружности с центром O. Докажите, что угол BFO – прямой.
Решение:
Заметим, что ∠ BCF = 180° – ∠ BEF = ∠ AEF, аналогично ∠ EAF = ∠ FDC, значит треугольник AEF подобен треугольнику DCF. Пусть K и L – середины отрезков AE и CD соответственно. Тогда ∠ AKF = ∠ FLB как углы между медианой и основанием в подобных треугольниках, поэтому точки B, K, F, L лежат на одной окружности. Но, так как серединные перпендикуляры к отрезкам AE и CD пересекаются в точке O, то точки K и L лежат на окружности с диаметром BO . Но тогда и точка F лежит на этой окружности, и ∠ BFO – прямой.
Задача 8:В микросхеме 2000 контактов, первоначально любые два контакта соединены отдельным проводом. Хулиганы Вася и Петя по очереди перерезают провода, причем Вася (он начинает) за ход режет один провод, а Петя – либо один, либо три провода. Хулиган, отрезающий последний провод от какого-либо контакта, проигрывает. Кто из них выигрывает при правильной игре?
Решение:Докажем, что выигрывает Петя. Мысленно разобьем контакты на четыре одинаковых группы A, B, C и D. В каждой группе пронумеруем контакты числами от 1 до 500. Петя будет отвечать на любой ход Васи так, чтобы для каждого номера k от контактов Ak, Bk, Ck и Dk отходило поровну проводов. До начала игры это условие, очевидно, выполняется. Именно благодаря этому условию у Пети всегда будет возможность ответить на ход Васи.
Теперь подробнее опишем Петину стратегию. Если Вася перерезает провод между контактами одной группы, например, провод AiAj, то Петя перережет провода BjBj, CiCj и DjDj. Если Вася перерезает провод между проводами из разных групп и с разными номерами, например, провод AiBj, то Петя в ответ перережет провода AjBi, CiDj и CjDi. Если же Вася перерезал провод между контактами из разных групп с одинаковыми номерами, например, провод AkBk, то Петя перережет провод CkDk. Заметим, что из описанной стратегии Пети следует, что провода, которые он собирается резать, не будут отрезаны до его хода.
Такие ходы Петя может сделать, так как из возможности отрезать один провод от некоторого контакта следует возможность отрезать по одному проводу от контактов с таким же номером. Отметим, что каждый раз после хода Пети от контактов Ak, Bk, Ck и Dk отходит поровну проводов. Значит, Петя всегда сможет сделать ход, и, так как количество проводов конечно, проиграет Вася.
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXV >> 9 класс | Убрать решения |