 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXVII >> 10 класс | Показать решения |
|
|
| XXVII всероссийская математическая олимпиада школьников. Заключительный этап. 10 класс |
|
|
Числа от 1 до 999999 разбиты на две группы: в первую отнесено каждое число, для которого болижайшим к нему квадратом является квадрат нечетного числа, во вторую – числа, для которых ближайшими являются квадраты четных чисел. В какой группе сумма чисел больше?
(Н. Агаханов)
Задача 2:На прямой выбрано 100 множеств A1,A2, … ,A100, каждое из которых является объединением 100 попарно непересекающихся отрезков. Докажите, что пересечение множеств A1,A2, … ,A100 является объединением не более 9901 попарно непересекающихся отрезков. (Точка также считается отрезком.)
(Р. Карасев)
Задача 3:Даны две окружности, касающиеся внутренним образо в точке N. Касательная к внутренней окружности, проведенная в точке K, пересекает внешнюю окружность в точках A и B. Пусть M – середина дуги AB, не содержащей точку N. Докажите, что радиус окружности, описанной около треугольника BMK, не зависит от выбора точки K на внутренней окружности.
(Т. Емельянова)
Задача 4:В стране несколько городов, некоторые пары городов соединены дорогами, причем между любыми двумя городами существует единственный несамопересекающийся путь по дорогам. Известно, что в стране ровно 100 городов, из которых выходит ровно по одной дороге. Докажите, что можно построить 50 новых дорог так, что после этого даже при закрытии любой дороги можно будет из любого города попасть в любой другой.
(Д. Карпов)
Задача 5:Многочлен P(x) = x³ + ax² + bx + c
имеет три различных действительных корня, а многочлен
P(Q(x)), где
Q(x) = x² + x + 2001, действительных корней не имеет.
Докажите, что
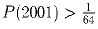 .
.
(Д. Терешин)
Задача 6:В магическом квадрате n × n, составленном их чисел 1,2, … ,n², центры любых двух клеток соединены вектором в направлении от большего числа к меньшему. Докажите, что сумма всех полученных векторов равна нулю. (Магическим называется клетчатый квадрат, в клетках которого записаны числа так, что суммы чисел во всех его строках и столбцах равны.)
(И. Богданов)
Задача 7:На высотах (но не на продолжениях высот) AA0,BB0,CC0 остроугольного треугольника ABC взяты точки A1,B1,C1, отличные от точки пересечения высот H, такие, что сумма площадей треугольников ABC1,BCA1,CAB1 равна площади треугольника ABC. Докажите, что окружность, описанная около треугольника A1B1C1, проходит через H.
(С. Берлов)
Задача 8:Найдите все натуральные числа n такие, что для любых двух взаимно простых делителей a и b числа n число a + b – 1 также является делителем n
(Д. Джукич)
| Задачная база >> Соревнования всероссийского уровня >> Заключительный этап всероссийской олимпиады >> XXVII >> 10 класс | Показать решения |