Задача 1:
Задача 2:
Существуют ли такие
действительные числа a, b и c (a ≠ 0), что при всех
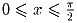
выполнено равенство
a sin 2x + b sin x + c = cos x?
Задача 3:
Задача 4:
На клетчатой доске
размером 1000 × 1000 стоят красные, синие и зеленые
фишки (в каждой клетке – не больше одной фишки).
Рядом (в соседних по стороне клетках) с любой
красной фишкой стоят 2 синие, а рядом с любой синей – 3 зеленые. Докажите,
что есть зеленая фишка, рядом с которой нет красных.
Задача 5:
Задача 6:
В тетраэдре ABCD угол
BAC равен углу ACD, а угол ABD равен углу BDC. Докажите, что
AB = CD.
Задача 7:
Пусть для каждого натурального n выражение T(n) обозначает длину периода
бесконечной десятичной дроби 1/n. Докажите, что для любого натурального
числа a выполнено неравенство
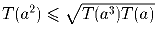
.
Задача 8:
Связный граф G остается связным при
удалении любых 18 вершин (вместе со всеми выходящими из них ребрами).
Назовем разрезом любое множество из 19 вершин, при удалении которых граф
теряет связность, а куском любую компоненту связности, которая образуется
при удалении разреза. Известно, что любой кусок, содержащий менее 10
вершин, не содержится ни в каком разрезе. Докажите, что никакой кусок не
содержится внутри разреза.


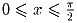 выполнено равенство
a sin 2x + b sin x + c = cos x?
Задача 3:
Задача 4:
На клетчатой доске
размером 1000 × 1000 стоят красные, синие и зеленые
фишки (в каждой клетке – не больше одной фишки).
Рядом (в соседних по стороне клетках) с любой
красной фишкой стоят 2 синие, а рядом с любой синей – 3 зеленые. Докажите,
что есть зеленая фишка, рядом с которой нет красных.
выполнено равенство
a sin 2x + b sin x + c = cos x?
Задача 3:
Задача 4:
На клетчатой доске
размером 1000 × 1000 стоят красные, синие и зеленые
фишки (в каждой клетке – не больше одной фишки).
Рядом (в соседних по стороне клетках) с любой
красной фишкой стоят 2 синие, а рядом с любой синей – 3 зеленые. Докажите,
что есть зеленая фишка, рядом с которой нет красных.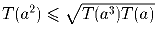 .
Задача 8:
Связный граф G остается связным при
удалении любых 18 вершин (вместе со всеми выходящими из них ребрами).
Назовем разрезом любое множество из 19 вершин, при удалении которых граф
теряет связность, а куском любую компоненту связности, которая образуется
при удалении разреза. Известно, что любой кусок, содержащий менее 10
вершин, не содержится ни в каком разрезе. Докажите, что никакой кусок не
содержится внутри разреза.
.
Задача 8:
Связный граф G остается связным при
удалении любых 18 вершин (вместе со всеми выходящими из них ребрами).
Назовем разрезом любое множество из 19 вершин, при удалении которых граф
теряет связность, а куском любую компоненту связности, которая образуется
при удалении разреза. Известно, что любой кусок, содержащий менее 10
вершин, не содержится ни в каком разрезе. Докажите, что никакой кусок не
содержится внутри разреза.