 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 4-й тур >> Высшая юниорская лига | Показать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Турнир матбоёв. 4-й тур. Высшая юниорская лига |
|
|
Назовем разбиение клетчатой доски 2000 × 2000 на доминошки (то есть прямоугольники из двух клеток) удачным, если любое разбиение этой доски на доминошки имеет с данным четное число общих доминошек. Сколько существует удачных разбиений?
Задача 2:Последовательность задана соотношениями
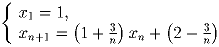
Докажите, что все ее члены – натуральные числа.
Задача 3:На окружности с центром в точке O даны точки A и B (не диаметрально противоположные). Через середину хорды AB проведена прямая, перпендикулярная AO и пересекающая окружность в точках K и N. Проведена прямая l, касающаяся окружности в точке B. Докажите, что окружность, описанная около треугольника KON, касается прямой l.
Задача 4:
Кузнечик прыгает по точкам интервала (0;1) по следующему правилу: из
точки x он может прыгнуть либо в точку  ,
либо в точку
,
либо в точку  .
Докажите, что можно покрасить конечное количество
отрезков суммарной длины не более
.
Докажите, что можно покрасить конечное количество
отрезков суммарной длины не более  в красный цвет так, что независимо от начальной
точки и направлений прыжков кузнечик рано или поздно попадет в красную
точку.
в красный цвет так, что независимо от начальной
точки и направлений прыжков кузнечик рано или поздно попадет в красную
точку.
Задача 5:
На сторонах треугольника ABC как на основаниях построены вовне равнобедренные треугольники ABC1, BCA1, CAB1 с углом 120 градусов при вершине. Докажите, что периметр треугольника A1B1C1 не больше периметра треугольника ABC.
Задача 6:
Докажите, что для любого многочлена P(x) с действительными коэффициентами существует такой многочлен Q(x) (также с действительными коэффициентами), что P(x) = Q(x + 1) – Q(x) для любого x.
Задача 7:
Известно, что a, b, c – целые числа, по модулю меньшие 2000. Докажите, что уравнение ax + by + cz = 0 имеет хотя бы два решения в целых числах, по модулю меньших 2000.
Задача 8:
В компании из 200 человек любых пятерых можно посадить за круглый стол так, чтобы каждый из них сидел между двух знакомых (предполагается, что если A знаком с B, то B знаком с A). Какое наименьшее число пар знакомых может быть в этой компании?
Задача 9:
Назовем клетчатый куб N × N × N хорошо упакованным ладьями, если в нем расставлены N² ладей, не бьющих друг друга. Дан хорошо упакованный ладьями куб со стороной 2n. Рассмотрим семейство кубов со сторонами 1, 2, 3,…, 2n, отложенных от одной из его вершин. Докажите, что количество хорошо упакованных ладьями кубов среди них не превосходит n + 1.
Задача 10:
Даны 12 палочек одинаковой длины. Можно ли распилить их на 39 частей, из которых затем удастся составить 13 равных прямоугольных треугольников (должны быть использованы все получившиеся части)?
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Турнир матбоёв >> 4-й тур >> Высшая юниорская лига | Показать решения |