 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Олимпиада >> 8-9 классы | Показать решения |
|
|
| Соревнования всероссийского уровня. Кубок памяти Колмогорова. IV кубок. Олимпиада. 8-9 классы |
|
|
Как разрезать таблицу по линиям клеток на пять прямоугольников, чтобы суммы чисел в каждом из них были равны? Укажите все способы и объясните, почему нет других.
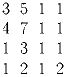
Задача 2:
Дан квадратный трехчлен P(x) = x² + bx + c. Известно, что P( – 10)P(10) > 0 и |c| > 100. Докажите, что этот трехчлен не имеет корней, лежащих между числами – 10 и 10.
Задача 3: Докажите, что натуральное число n является составным тогда и только тогда, когда существуют такие натуральные числа a, b, x и y, что a + b = n и
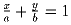 .
.Задача 4:
Точка P внутри треугольника ABC такова, что угол PBA равен углу
PCA и втрое меньше суммы углов B и C треугольника. Докажите, что
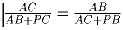 .
.
В компании из n человек, где каждый знаком хотя бы с одним из
остальных, у всех поровну знакомых (считается, что если A знаком с B,
то и B знаком с A). Докажите, что из членов этой компании можно
выбрать не менее, чем 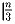 непересекающихся пар знакомых.
непересекающихся пар знакомых.
Задача 6: Точки K и L – проекции вершин A и C остроугольного треугольника ABC на биссектрису внешнего угла при вершине B. Точки H и M – основания высоты и медианы, проведенных из вершины B. Докажите, что точки H, M, K и L лежат на одной окружности. Задача 7: Найдите все пары целых чисел (x,y), для которых x²(y – 1) + y²(x – 1) = 1. Задача 8: На клетчатой бумаге отмечены 49 узлов сетки, расположенные в виде квадрата 6 × 6. Какое минимальное число единичных отрезков с концами в отмеченных узлах нужно провести, чтобы между любой парой соседних узлов был путь не длиннее 3?
| Задачная база >> Соревнования всероссийского уровня >> Кубок памяти Колмогорова >> IV кубок >> Олимпиада >> 8-9 классы | Показать решения |