Задача 1: Среди первых 60 натуральных чисел произвольно выбрано 30 + n (где 1 ≤ n ≤ 30) различных чисел. Докажите, что среди выбранных чисел всегда найдутся 2n чисел таких, что их сумма равна 61n. (C. С. Тасмуратов)

Задача 2: Решите в натуральных числах x, y, z и t уравнение x² + y² + z² = 2^t.

(В. В. Произволов)

Задача 3: Играя в домино, Мустафа, Табриз, Гамид и Эльмир взяли по семь костей с различной суммой очков. При этом сумма очков Мустафы и Табриза оказалась равной сумме очков Гамида и Эльмира, а разница очков Мустафы и Табриза составила 27/7 разницы очков Гамида и Эльмира. Укажите какие-нибудь 12 костей домино, которые находятся на руках у Мустафы и Табриза.

(Р. Мустафаев)

Задача 4: Из бумаги склеили правильный тетраэдр. Разрежьте его на 12 одинаковых бумажных равносторонних треугольников.

(В.В.Произволов)

Задача 5: Могут ли длины сторон x, y и z какого-нибудь треугольника удовлетворять неравенству: x³ + y³ + z³ + 2xyz ≥ x²(y + z) + y²(z + x) + z²(x + y)?

(Д.А.Калинин)

Задача 6: У крестообразно пересекающихся четырехугольников соответствующие стороны параллельны и отстоят друг от друга на расстояние 1. Докажите, что периметры четырехугольников равны. (В. В. Произволов)

Задача 7: В некоторых клетках шахматной доски проведена одна из двух возможных диагоналей так, что ни для каких двух диагоналей концы их не совпадают. Какое наибольшее количество диагоналей можно провести, соблюдая такое условие?

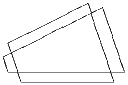
(И. Ф. Акулич)

Задача 8: Дан выпуклый шестиугольник ABCDEF, в котором AB = CD = EF,  ∠ A =  ∠ C =  ∠ E и  ∠ B =  ∠ D =  ∠ F. Докажите, что BC = DE = FA. (В. В. Произволов)