 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Турниры журнала ``Квант'' >> Математика 6-8, 2001 >> Вариант 3 | Убрать решения |
|
|
| Заключительный конкурс "Математика 6-8" журнала "Квант". Вариант 3 |
|
|
(И. Акулич)
Задача 2: В равнобедренном треугольнике ABC (AB = BC) проведена биссектриса AM. Найдите углы треугольника, если известно, что BM = AC. (Д. Калинин) Задача 3: Решите систему уравнений: x(1 + y1/2) = y(1 + z1/2) = z(1 + x1/2) = 2 Задача 4: Пусть M – конечное подмножество множества целых чисел, причем количество элементов в M кратно четырем, а между любыми двумя числами, не принадлежащими M, расположено четное количество элементов из M. Докажите, что M можно разбить на две части с равным числом элементов и равной суммой.(С.Волченков)
Задача 5: Клетчатый прямоугольник 2 × 3 сложен из 17 спичек, как показано на рисунке. Какие размеры может иметь клетчатый прямоугольник, составленный из 1000 таких же спичек?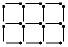
(А. Шаповалов)
Задача 6: На стороне AB равностороннего треугольника ABC, отмечена точка C1, а на стороне AC – точка B1 так, что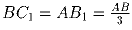 ; M –
точка пересечения отрезков BB1 и
CC1. Найдите угол ANC.
; M –
точка пересечения отрезков BB1 и
CC1. Найдите угол ANC.
(Д. Калинин)
Задача 7: Можно ли в кубе с ребром 2000 разместить 7 точек так, чтобы расстояние между любыми двумя было бы больше 2001? Точки можно помещать и на поверхности куба.(С.Волченков)
Задача 8: Целые числа x, y, z таковы, что числа xy + 1, yz + 1 и zx + 1 являются полными квадратами. Докажите, что произведение xyz делится на 8.
(В.Сендеров)
| Задачная база >> Соревнования всероссийского уровня >> Турниры журнала ``Квант'' >> Математика 6-8, 2001 >> Вариант 3 | Убрать решения |