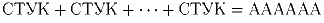
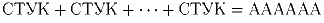Задача 1: При каком наименьшем числе слагаемых возможно равенство ? (Одинаковым буквам соответствуют одинаковые цифры, разным – разные.)

Задача 2: Торт имеет форму выпуклого пятиугольника со свечами в вершинах. Обязательно ли на торте найдется точка, начиная из которой прямыми разрезами торт можно разделить на пять частей одинаковой площади, в каждой из которых есть свеча?

Задача 3: Король обошел все поля шахматной доски, побывав на каждом поле по одному разу. Когда соединили центры полей, по которым он последовательно проходил, получилась ломаная без самопересечений. Найдите наибольшее возможное число диагональных ходов.

Задача 4: Окружность пересекает все стороны треугольника. Докажите, что ее радиус больше радиуса окружности, вписанной в треугольник.

Задача 5: При вычислении на калькуляторе суммы ста слагаемых Петя несколько раз ошибался, сдвигая в слагаемом запятую на один знак – иногда вправо, иногда влево. Мог ли результат оказаться вдвое больше правильного?

Задача 6: Найдите наименьшее делящееся на 99 натуральное число, все цифры которого четны.

Задача 7: Концы каждого из 51 отрезков расположены на двух противоположных сторонах прямоугольника и делят каждую на 50 равных частей (вершины прямоугольника – тоже концы отрезков). Докажите, что среди отрезков есть равные.

Задача 8: Два игрока по очереди красят стороны 37-угольника так, чтобы никакие соседние стороны не оказались одноцветными. Игра заканчивается, когда окрашены все стороны. Проигрывает тот, кто последним использовал новый цвет. Кто из игроков может обеспечить себе победу?