 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XIV турнир (ноябрь, 1999) >> Турнир матбоёв >> Математический бой N4 >> Старшая группа, высшая лига | Показать решения |
|
|
| XIV Уральский турнир юных математиков. Турнир матбоёв. Математический бой N4. Старшая группа, высшая лига |
|
|
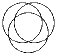
На плоскости нарисованы три окружности так, как показано на рисунке. Вначале в каждой из семи частей, на которые они делят плоскость, стоит по единице. За один ход разрешается выбрать одну из окружностей и либо сменить знаки всех стоящих внутри нее чисел, либо возвести все эти числа в квадрат. Можно ли за несколько таких ходов добиться ситуации, когда в центральной области стоит – 1, а во всех остальных – единицы?
Обозначим через π (n) количество простых чисел, не превосходящих n. Докажите, что π (2n) + π (n! + n) ≥ π (n) + π (n! + 2n).
Задача 3:
На планете 10000 городов, среди которых есть столицы государств. Некоторые города связаны дорогами так, что любая дорога соединяет ровно два города, и от любого города до любого другого можно добраться по дорогам. При этом, чтобы попасть из одной столицы в другую, нужно проехать не менее 200 дорог. Докажите, что на планете меньше 100 столиц.
Задача 4:
На доске написаны числа 2, 3, 9. Разрешается заменить любые два
числа а и b на числа 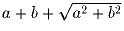 и
и
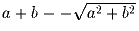 . Может
ли на доске когда-нибудь появиться число, меньшее 1?
. Может
ли на доске когда-нибудь появиться число, меньшее 1?
Задача 5:
Верен ли признак равенства треугольников по двум высотам и медиане, проведенной к третьей стороне?
Задача 6:
От картонного треугольника прямолинейными разрезами один за другим отрезают одинаковые треугольники. Найдется ли треугольник, для которого это удастся сделать хотя бы 13 раз?
Задача 7:
На столе лежат 9 карточек, на которых написаны натуральные числа от 1 до 9. Двое по очереди берут карточки со стола. Побеждает тот, кто первым сумеет составить из своих карточек, знаков арифметических действий ( + , – , × , : ) и скобок выражение, значение которого равно 40. Если по окончании игры такого выражения не может составить ни один из играющих, то считается, что игра закончилась вничью. Кто выиграет при правильной игре: тот, кто делает первый ход, или его партнер?
Задача 8:
При каком наибольшем k существуют k подряд идущих натуральных чисел таких, что их суммы цифр являются перестановкой k подряд идущих натуральных чисел?
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XIV турнир (ноябрь, 1999) >> Турнир матбоёв >> Математический бой N4 >> Старшая группа, высшая лига | Показать решения |